This is the second part of a series. See parts 1, 3, 4, and 5.

When economics tried to put itself on a scientific basis by recasting utility in strictly ordinal terms, it threatened to perfect itself to uselessness. Summations of utility or surplus were rendered incoherent. The discipline’s new pretension to science did not lead to reconsideration of its (unscientific) conflation of voluntary choice with welfare improvement. So it remained possible for economists to recommend policies that would allow some people to be made better off (in the sense that they would choose their new circumstance over the old), so long as no one was made worse off (no one would actively prefer the status quo ante). “Pareto improvements” remained defensible as welfare-improving. But, very little of what economists had previously understood to be good policy could be justified under so strict a criterion. Even the crown jewel of classical liberal economics, the Ricardian case for free trade, cannot meet the test. As John Hicks memorably put it, the caution implied by the new “economic positivism might easily become an excuse for the shirking of live issues, very conducive to the euthanasia of our science.”

Hicks, following Nicholas Kaldor and Harold Hotelling, thought he had a way out. Suppose there were an economy that, in isolation, could produce 50 bottles of wine and 40 bolts of cloth. If the borders were opened, the country would specialize in wine-making. Devoting its full capacity to the task, it would produce enough wine so as to be able to keep 60 bottles for domestic use, even while trading for a full 50 bolts of cloth. Under the presumption that people prefer more to less, “the economy” would clearly be made better off by opening the borders. There would be more wine and more cloth “to go ’round”. However, in practice, skilled cloth-makers would be impoverished by the change. They would be reemployed as menial grape-pickers, leading to a reduction of earnings so great that they’d have less cloth and less wine to consume, despite the increase in overall wealth. Opening the borders is not a Pareto improvement: the “pie” grows larger, but some people are made badly worse off. So, on what basis might a “scientific” economist recommend the policy?

The insight that Kaldor, Hicks, and Hotelling brought to the problem is simple. Opening the borders represents a potential Pareto improvement, if we imagine that those who benefit from the change compensate those who lose out. In our example, since the total quantities of wine and cloth available are greater with free trade than without, there must be some way of distributing the bounty that leaves everyone at least as well off as they were before, and others better off. Economists could, in good conscience, argue for policies that would be Pareto improvements, if they were bundled with some redistribution, regardless of whether or not the redistribution would, in the event, actually happen. Such a change is now said to be “Kaldor-Hicks efficient“, or, more straightforwardly, a “Potential Pareto improvement”.

At first blush, this sounds dumb. Nobody harmed by a change can eat a “potential” Pareto improvement. But there is, nonetheless, a case to be made for the criterion. The distribution of scarce goods and services is inherently a question of competing values. But quantities of goods are objective and measurable. So a “scientific” economics could concern itself with “efficiency” — maximizing objective economic output, while the distribution of that output and concerns about “equity” could be left to the political institutions that adjudicate competing values. An activity that could leave everybody with all the goods and services they might otherwise have while providing some people with even more necessarily implies an increase in the quantity of goods and services made available, and is objectively superior on efficiency grounds. If those goods and services get distributed poorly, that may be a terrible problem. But it represents a failure of politics, and outside the scope of a scientific economics. Let economics concern itself with the objective problem of maximizing output, and remain silent on the inherently political question of how output should be distributed.

This is might be a clever answer to the threat of the “euthanasia of our science”, but it is incoherent as the basis for a welfare economics. In reality, economic output cannot be objectively measured. The quantity of corn or cars or manicures produced can be counted. An action that increases the availability of all goods, actual and potential, might be pronounced an objective increase in the size of the economy. But most economic activities provoke tradeoffs in production: more of something gets produced, while less of something else does. There is no way to determine whether such an event represents an increase or decrease in the size of the economy without making interpersonal comparisons of value. Dollar values can’t be used in place of goods and services unless the dollars actually change hands, prices change to reflect the new patterns of wealth and production, and all parties consent that their new situation is superior to the old. When there are trade-offs made in patterns of production, only an actual Pareto improvement counts as an objective increase in the size of an economy.

Tibor de Scitovsky demonstrated very elegantly the incoherence of Kaldor-Hicks efficiency in a world with multiple goods. I’m going to present the argument in detail, stealing a pedagogical trick from Matthew Adler and Eric Posner, but adding my own overdone diagrams.

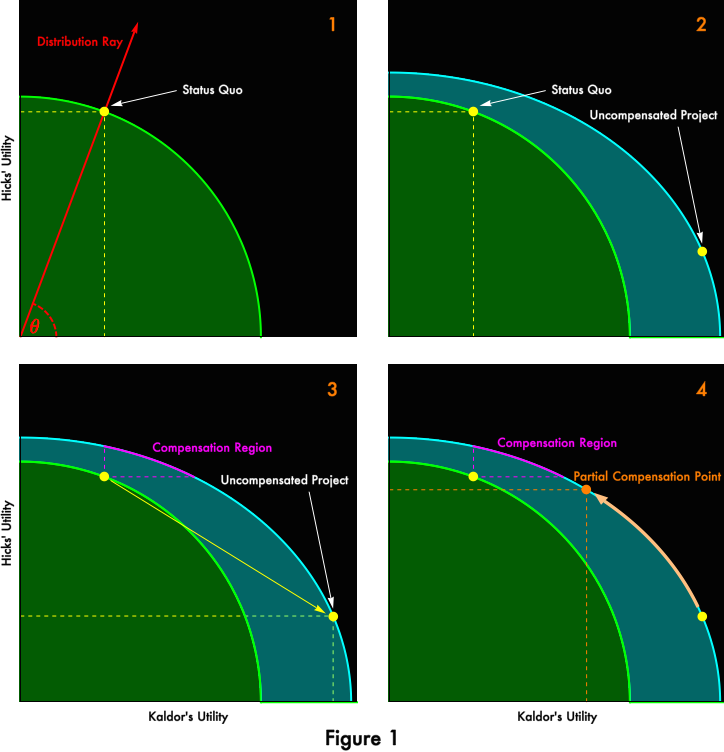
Let’s start charitably. Figure 1 shows some pictures of the special case that might be scored as an objective increase in efficiency:

We have an economy of two people, Nicholas Kaldor and John Hicks. In Panel 1, the bright green curve represents a “utility possibilities curve“. For each point on the curve, the x value represents “how much utility” Kaldor enjoys while the y value represents how much Hicks enjoys. Utility is strictly ordinal, so the axes are unlabeled, and the exact shapes are meaningless. You could stretch or squeeze the diagram as much as you like, rescale it to any aspect ratio, and nothing would change. Any transformation that preserves the x– and -ordering of things is fine.

At a given time, the economy is represented by a point on the curve. Each location reflects a different distribution of economic output. The point where the curve intersects the y-axis represents an economy in which Hicks gets literally all of the goods, while Kaldor dies starving. As we rotate clockwise along the curve, Hicks gets less and less, while Kaldor gets more and more. Again, the exact shape is meaningless. All we can tell is that, as control over economic output shifts, Hicks’ utility declines while Kaldor’s rises. Finally we reach the x-axis, where it is Kaldor who starves while Hicks feasts. At the moment, the economy sits at the yellow point marked “status quo”.

A distribution can be summarized by the angle marked θ in Panel 1. When θ is 0°, Kaldor owns the whole economy. When θ is 90°, Hicks owns everything. We can locate Kaldor’s and Hicks’ satisfaction under any distribution by following the “distribution ray” to the utility possibilities curves. [1]

In Panel 2, a policy change is proposed. It might be deployment of a new technology, or construction of high return infrastructure. But let’s imagine that it trade-liberalization under circumstances where Ricardian comparative advantage logic unproblematically holds.

It turns out that John Hicks is a skilled cloth-maker. That’s how he earns an honest living. If trade were liberalized, textile manufacture would be outsourced, and he would be out of a job. Nicholas Kaldor, on the other hand, owns acres and acres of vineyards. His real income would dramatically increase, as cloth would grow cheaper and the market for his wine would expand. If the borders were simply thrown open, the economy would end up at the position marked “Uncompensated Project” in Panel 2. Trade liberalization is not Pareto improving. As you can see, relative to the status quo, we shift rightwards (Kaldor benefits big time!) but also downwards (Hicks loses) if the project is implemented without compensating redistribution. Can we state, as a matter of objective science rather than value judgment, that trade-liberalization would represent an efficiency improvement?

Kaldor, Hicks, and Hotelling ask us to perform a thought experiment represented on Panel 3. Suppose that we did throw open the borders. We’d be thrust along the yellow arrow from the current status quo to the new “uncompensated project” point. Would it be possible to redistribute along the new utility possibilities frontier in a way that would render the policy-change-plus-redistribution a Pareto improvement, a boon both for Kaldor and for Hicks? The existence of the purple region, above and to the right of our original status quo, shows that it is indeed possible. Our trade liberalization is a “potential Pareto improvement”, and should be scored by economists an objective efficiency gain, regardless of whether not the political institutions that adjudicate rival claims actually impose compensation. Political institutions might not compensate Hicks at all, leaving him where he lands in Panel 3. Or they might compensate only partially, as in Panel 4. Maybe it is best to retain market incentives for fogies like Hicks to anticipate change and learn new skills. Maybe the resentment that would be provoked by full compensation overwhelms the benefit of making Hicks whole. Maybe there is no good reason, but the political system is plagued by inertia and so fails to compensate. Or maybe Kaldor has bought the politicians with his good wine. Those are questions beyond the scope of economic science. Nevertheless, say Kaldor, Hotelling, even penurous Hicks, we can objectively declare the proposed policy an efficiency improvement. If poor Hicks starves when all is said and done, well, that will be the fault of the politicians. Or perhaps it will be optimal. As economists, we really can’t say. Incomparable subjectivities are involved.

I have to admit to feeling queasy about this, like a surgeon who opens the chest of an awake screaming patient and then blames the anesthesiologist for sleeping in. But this is the procedure Kaldor and Hicks propose for us. (Hotelling, to his great credit, admits the possibility that imperfect politics might imply revision of his economic prescriptions.) But we’ll put our reservations aside for now, and declare this policy change an “efficiency increase”, distinct and separable from distributional concerns.

Now let’s examine a different project. Hicks has abandoned his cloth-making (a folly of youth!) and has entered a respectable profession, bourbon distillery. Kaldor, never a fool, has stuck with his wine-making.

Here is the thing, though. Each gentleman has come to despise the good he himself produces. The grapes stain Kaldor’s fingers, his clothes, his bare soles. Hicks is plagued by the smell of corn mash and the weight of oak barrels. If Hicks were a rich man, he’d never look at a bottle of bourbon. He’d sip wine like a gentleman. If Kaldor were a rich man, he would drown the nightmares (out, out, damned wine stain!) in a bottle of whiskey.

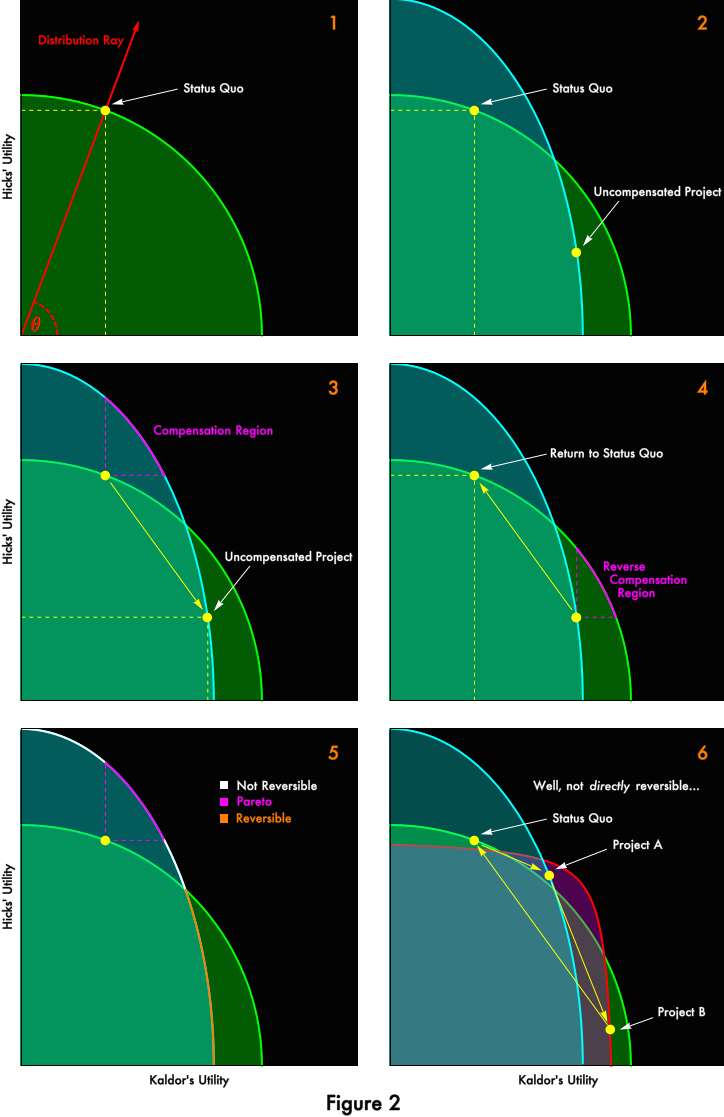
In Panel 1 of Figure 2, we start very much like before. Kaldor and Hicks ply their trades, they get what they get, represented in joint utility terms by the yellow-dot status quo.

In Panel 2, a rezoning of some land is considered, which would prevent “industrial agriculture” on acreage currently devoted to the growing of corn. There’d be nothing for this land but to transition it to bucolic vineyards. Both of our protagonists are ambivalent about the proposal. In his role as producer, the rezoning would be great for Kaldor’s business. Hicks would have to sell the land for a song, enabling more and cheaper wine production. But the rezoning would shift the composition of output in a manner opposed to Kaldor’s consumption preferences. If Kaldor could be made rich in some manner independent of the proposed change — if we drew a “distribution ray” in Panel 2 at 0° signifying Kaldor’s complete ownership of output — Kaldor would strongly prefer the status quo and the abundant bourbon it produces to the proposed repurposing of land for wine. Conversely, the businessman in Hicks hates the proposal, selling out to Kaldor for a song would really sting! But the wine-lover in Hicks would be delighted, if only he’d be rich enough to afford the wine. If the “distribution ray” were at 90° — if Hicks was very rich — he’d strongly prefer that the land be rezoned!

So, can economic science tell us whether the rezoning is efficient? According to Messrs. Kaldor, Hicks, and Hotelling (when they dabble at economics), the proposal is efficient. In Panel 3, you can see that, subsequent to the rezoning, it would be possible to redistribute output in a manner that would leave both parties better off than the status quo, exactly as in Panel 3 of Figure 1 above! The change would survive any cost-benefit analysis.

But. Here comes Mr. Scitovsky, who is a real sourpuss. He points out (Panel 4) that, subsequent to the rezoning, analysis under the very same criterion would declare a reversal of the rezoning efficient! Does it make sense to declare the rezoning an “increase in economic efficiency” and then to declare the undoing another increase in economic efficiency? I have an idea: Get the zoning authority to to re-re-re-re-re-re-rezone the land. We’ll have so many economic efficiency increases, all scarcity will be vanquished!

Or not. What Scitovsky showed, quite definitively, is that the Potential Pareto criterion is incoherent as a measure of economic efficiency. It just doesn’t work. In a fallen world, it may in practice be used to evaluate potential changes, just as in a fallen world interpersonal comparisons of utility are used to evaluate changes. Both are equally (un)scientific under the axioms of liberal economics. Scitovsky proved that, in general, it is simply not possible to score the efficiency of a change without taking into account effects both on output and on distribution. The two are not independent, except in the special case illustrated by Figure 1.

Scitovsky didn’t think he was destroying the Potential Pareto criterion entirely. He pointed out that, for some distributions, reversals are not possible. Panel 5 of Figure 2 divides the utility possibilities frontier after the proposed change into distributions that are Pareto-improving (which implies making actual, full compensation for the change), into regions that are reversable and therefore not rankable as efficiency improvements, and into regions that are Potential Pareto but not Pareto and still irreversible. Scitovsky thought that changes that led to these distributions might still scored as efficiency increasing under Kaldor-Hicks-Hotelling logic. It took subsequent work to show that, no, even these irreversible regions aren’t safe. (See Blackorby and Donaldson for a mathematical review.) Scitovsky’s proposed modification of the Kaldor-Hicks criterion is intransitive, permitting cycles if more than two projects are compared. Project A can be “more efficient” than the status quo, Project B can be “more efficient” than Project A, but the status quo can be “more efficient” that Project B. Hmm. Panel 6 of Figure 2 shows an example. I won’t go through it in detail, but if you’ve understood the diagrams, you should be able to persuade yourself that 1) each transition is both Kaldor-Hicks efficient and irreversible; 2) there is no coherent efficiency ordering between them.

While it is impossible to rank alternatives at arbitrary distributions, it is possible to rank projects if we fix a distribution. In Figure 2, Panel 2, extend a “distribution ray” outward from the origin at any angle. The outermost project is preferred. At a slight angle, when Kaldor enjoys most of the output, the bourbon-producing status quo is preferable. At a steep angle, when it is Hicks who will do most of the consuming, the wine-drenched rezoning is preferable. There is some distribution where both Kaldor and Hicks would be indifferent to the proposed rezoning, where the curves cross.

Given the rather elaborate story we told to rationalize the shape of the curves in Figure 2, you might wonder whether we might rescue a “scientific” efficiency from value-laden distributional concerns by suggesting that these “reversals” and “intransitivities” are rare, pathological cases that can in practice be ignored. They are not. We will encounter a simpler example soon. The likelihood that these sorts of issues arise increases with the number of people and goods in an economy, unless you restrict the form of peoples’ utility functions unrealistically. Allowing for (nearly) unrestricted preferences (people are assumed always to prefer more goods to less or to have the option of “free disposal”), the only projects that can be ranked independently of distribution are those that increase the number of some goods and services without any cost in availability of other goods or services, an analog to Pareto efficiency in the sphere of production.

As one economist put it:

The only concrete form that has been proposed for [a social welfare function grounded in ordinal utilities] is the compensation principal developed by Hotelling. Suppose the current situation is to be compared with another possible situation. Each individual is asked how much he is willing to pay to change to the new situation; negative amounts mean that the individual demands compensation for the change. The possible situation is said to be better than the current one if the algebraic sum of all the amounts offered is positive. Unfortunately, as pointed out by T. de Scitovsky, it may well happen that situation B may be preferred to situation A when A is the current situation, while A may be preferred to B when B is the current situation.

Thus, the compensation principal does not provide a true ordering of social decisions. It is the purpose of this note to show that this phenomenon is very general.

That economist was Kenneth Arrow. “This note“, circulated at The Rand Corporation, was the first draft of what later become known as Arrow’s Impossibility Theorem.

It is not, actually, an obscure result, this impossibility of separating “efficiency” from distribution. The only place you will not find it is in most introductory economics textbooks, which describe an “equity” / “efficiency” trade-off without pointing out that the size of the proverbial pie in fact depends upon how you slice it.

I wonder why that is missing.

---

Note: This was the second of a series of posts on welfare economics. The first was here. With apologies, I’m disabling comments until the end of the series, so I can get through my little plan untempted by the brilliant and enticing diversions that I know commenters would offer. Please do write down your comments, and save them for the final post in the series. I thought this would go faster; I feel very guilty for leaving no forum for responses for so long. I really am sorry about that!

---

This entry was posted on Thursday, June 5th, 2014 at 7:32 am PDT.
You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.