I’ve been trying to develop my intuitions about how inequality might affect aggregate growth. It’s not like this is a new question. Theoretical arguments have been made both ways, and an empirical literature found a consensus in the 1990s (inequality looked bad for growth), then squinted harder to find little relationship in the 2000s. For some careful theorizing about how inequality might harm growth, take a look at this paper by Philippe Aghion, Eve Caroli, and Cecelia Garcia-Penalosa (“ACG”). They tell three stories, with very careful models: i) when capital markets are imperfect, inequality might reduce the efficiency of investment, as the less productive opportunities of the wealthy are funded in preference to the more productive opportunities of the poor; ii) the borrowing required to fund investment under inequality impose agency costs, because entrepreneurs expend less effort when the benefits and costs of their labors are shared with financiers; and iii) unequal access to investment opportunities may combine with financial market imperfections to create macroeconomic downcycles during which savings cannot be efficiently invested.
Those are good stories, and there are others. The oldest story has to do with incentives. The traditional notion of a trade-off between efficiency and equity comes from the idea that redistribution blunts incentives to invest and produce. In almost any model, reducing after-tax returns on investment will reduce investment, ceteris paribus. It is worth pointing out that inequality and redistribution are separate questions. Inequality may be harmful (or helpful) to growth regardless of whether redistribution by the state would would be good policy. That lower after-tax investment returns reduce growth doesn’t really tell us all that much about the effect of inequality. Also, incentives swing both ways: see ACG story (ii) above, or models of effort in tournaments (e.g. Freeman & Gelber via Benign Brodowicz and commenter Indy).
Anyway, there are lots of stories. I want to add one more, and illustrate it with a very simple model. My intuition goes like this: when people are relatively poor, they spend nearly all their income on real goods and services with care, in ways that yield positive returns in present and future consumption. As people grow wealthy, they spend an increasing fraction of their wealth on financial assets, purchases of which only imperfectly translate to productive mobilization of real goods and services. To make my life as a modeler easier, I conjecture that financial assets are phenomenally inefficient — not only do they fail to yield any positive return, but the net expenditure of real goods and services for financial assets is “thrown into the sea”. We’ll see that despite this, under not-entirely-outrageous assumptions, it might be optimal for wealthy agents to purchase an ever larger “stock” of financial assets, but that by doing so rather than mobilizing real resources, they exert a drag on aggregate growth. We’ll find that transfers (or zero-interest loans) of real resources from the issuers of financial assets to the relatively poor can restore growth, and be Pareto optimal if no deductions are made from the claims of the wealthy when real resources are transfered to the poor. In other words, printing money and giving it to poor people (who then buy real resources from the rich, who prefer the insurance value of money to the use value of their marginal goods) can be optimal and noninflationary. We’ll also find that if there is a monopoly issuer of conventionally “safe” financial assets, the value of those assets can be kept stable even if the issuer totally wastes the real resources it receives in exchange for them, and even if the waste and “insolvency” of the issuer is widely known. Effectively, an arbitrarily insolvent Ponzi scheme can be sustained indefinitely due to the usefulness of having a conventional financial claim that agents can use to pool idiosyncratic risks which they cannot contract to diversify. However, if the economy suffers a shock deep enough not only to halt but to reverse the steady state net positive flow of real goods and services from the economy, a devaluation (inflation) or collapse might occur.
This is a shitty little model, not anything an economist would take seriously. Like most models, it’s tendentious — I set out to confirm my intuition that inequality dampens growth via a financial channel, and I’ve done so. Nevertheless, this what I’ve been thinking about lately, and it’s led me to some unexpected conjectures about money. Please read it, if you must read it at all, as a sketchy first draft. (i know, i am such a girl i’ll never change the world.)
Here’s the setup. There’s a population of rational, risk-averse, agents. At any point in time, each agent can exchange goods and services with other agents, or surrender some of their stuff to a monetary authority (government/banking system) to build a stock of money. (When agents trade amongst themselves, it doesn’t matter whether they use money as a medium of exchange, any money holdings are transient.) The exchange and use of real stuff yields a positive instantaneous return on average, but is risky: sometimes real activity works out, but sometimes it fails. The exchange rate between money and real goods and services — the price level — is notionally fixed. We’ll return to the question of whether this presumption of price stability is credible (without state coercion), since monetary claims will be backed by nothing. We simply assume that, as our story begins, agents believe the price level to be stable. Therefore, they view money as a risk-free asset (that pays no interest; the risk-free rate in our economy is zero). Money is the only financial asset: agents can’t buy or sell claims on one another’s production. So agents cannot diversify their exposure to the risk of their real projects. They must decide at each point in time how much of their wealth to plow into risky real stuff, and how much to allocate to safe money. By assumption, there is no systematic risk: individual project returns are uncorrelated. Agents seek to maximize return while managing undiversifiable idiosyncratic risk.
Some technical points (you can skip this paragraph!): Because it makes the math easy, I’ll model returns as normal, and individual agents as having “constant absolute risk aversion (CARA / negative exponential) utility”. I don’t think the assumption of normal returns hurts us much. (This isn’t like a pricing model where fat tails can kill us — fatter tails would just make our agents look more risk-averse and hold more money.) The CARA assumption is less defensible for the very reason it makes the math easy: Under CARA utility, an agent choosing between a high-return risky and low-return risk-free asset always wants to hold a fixed quantity of the risky asset. That’s unrealistic — even at high levels of wealth, I think people typically expand their holdings of risky assets in absolute terms as they grow richer, although they diminish risky holdings as a proportion of their overall portfolio. That is, it’d be more realistic to use a DARA/IRRA utility function, but with the ones I’ve tried, the math is too hard. Qualitatively, though, this doesn’t matter very much. If agents increase their risky holdings in fixed proportion with their wealth or faster (CRRA or DRRA preferences) my story on inequality breaks down (or reverses under DRRA). But as long as agents put an ever greater fraction of their wealth into money-like assets as they grow rich (and I think they do, for informational as well as risk-management reasons), the basic results holds. The curves below with “kinks” would be smoother under a more realistic DARA/IRRA utility function, but the qualitative implications would not change.
Without further ado, here are some pictures.
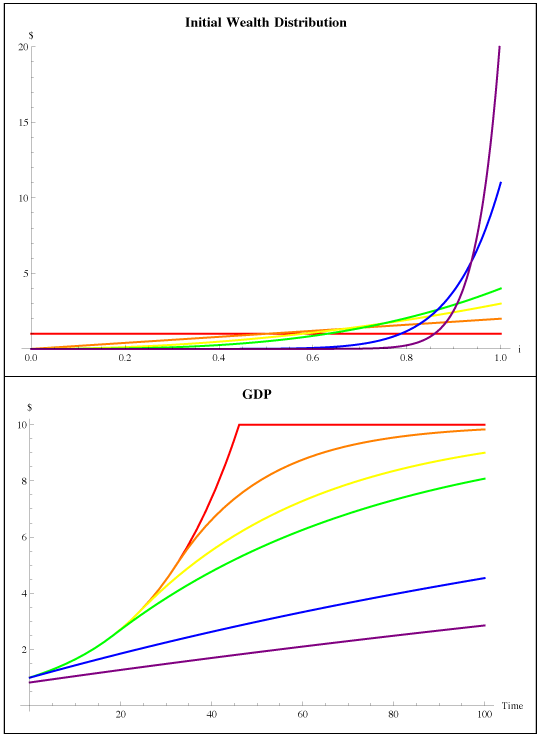
The top graph displays several initial wealth distributions. Imagine a large population of individuals lined up from poorest to richest, with wealth rising from left to right. The flat, red line represents perfect equality. The purple line represents a highly unequal distribution. The bottom graph displays the expected evolution of GDP for each of those distributions. (Curves are matched to income distributions by color throughout.) Eventually the economy reaches a steady state, in this case at GDP of 10 (an arbitrary quantity). But the more equal distributions reach the steady state more quickly than the unequal distributions, because wealthier people exchange part of their wealth for money rather than putting it to productive use in the real economy.
It might seem odd and unrealistic to imagine an economy that just “tops out” and stops growing. This happens because I haven’t modeled technological change. We can easily augment the model with exogenous growth in technology. The easiest way to do that would be to let both investment returns and absolute risk tolerance grow with technology (that is, to let the numeraire be technology adjusted), and set the risk-free rate to the rate of technology growth. Then we get the more comforting graphs below. We could make other choices about how to model technology, “endogenize” it or rethink how technology affects agent preferences, but that’s not what we’re after right now.
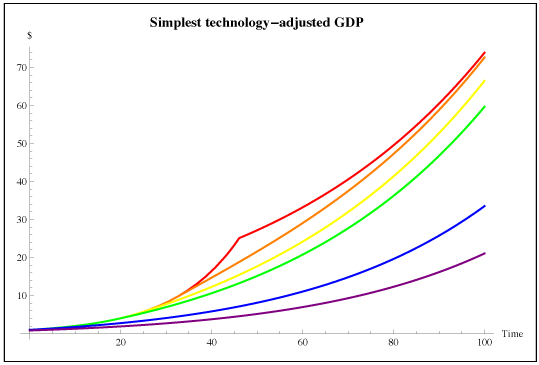
Let’s return to the simple, constant-technology model, and see what happens to money. In the graph below, the solid line represents the aggregate perceived wealth of agents in the economy. The dashed line represents real income, GDP, the goods and services that the economy is actually producing. The gap between the solid and dashed line is the stock of money, backed by nothing but nevertheless part of the perceived wealth of agents in the economy.
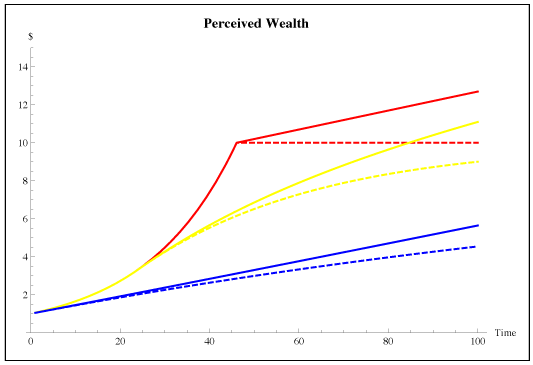
Note that the money stock grows earlier in less equal economies. This is the “leakage” that slows their growth. But for all economies, money growth is unbounded, while (technology-adjusted) GDP approaches a steady state. That is, for all economies, eventually the stock of money gets to be much, much larger than the capacity of the economy to produce goods and services. Is it rational, then, for agents to keep adding to their money stock? Can this be a stable arrangement?
The surprising answer is yes, as long as there is no other risk-free asset in the economy. By assumption, agents who choose not to hold money bear idiosyncratic risk: the value of their holdings, while expected to increase, fluctuates in a manner that they dislike. As long as all agents treat money — backed by nothing at all — as a risk-free asset, and there are many agents whose risks are uncorrelated, each agent knows with almost-certainty that whenever their real projects fail, others will have succeeded more than enough so that the flow of goods and services to the monetary authority will be more more than sufficient to accommodate their idiosyncratic withdrawals. As long as the net flow into money is positive at all times, the aggregate stock money is irrelevant. Each agent values her own stock of money, and wants more, because the greater her stock, the greater her entitlement to make withdrawals should she encounter a string of bad events. The growing illusion of wealth produces real benefits, by leaving agents less insecure than they otherwise would have been. The economy is effectively a Ponzi scheme that, under our assumptions, never fails. More formally, it is a Nash equilibrium: each agent’s best strategy, under the assumption that other agents treat money as a stable risk-free asset, is to treat money as a stable risk-free asset. This is true even when all agents are fully aware of the Ponzi-ish nature of the arrangement.
Of course, this benign result depends upon several assumptions, some of them not so realistic. We’ve assumed that all real investments are uncorrelated and money is the only financial asset. If real investment returns are correlated — if there is systematic risk — it is possible there would be a period during which there would be more losses than gains on real investments. Then, rather than happily exchanging goods and services for money, agents in aggregate would try to redeem money for stuff that financial asset issuers don’t actually have. What then? Our model can’t help us — its assumptions are violated at this point, money is no longer a risk-free asset. The value of financial assets could simply collapse à la Bernie Madoff. But qualitatively, if agents can be made to believe that money will continue to offer some insurance value (and if the expected return on unplanned real investment is low and/or the risks are high), then real goods and services could become more expensive in terms of money until the net flow into financial assets matched the net flow out. Rather than a collapse, there would be an inflation. Here the stock of money matters: under almost any circumstance, dollars offer diminishing marginal insurance value. If there is a large stock of dollar claims, then the devaluation required to match inflows and outflows would have to be larger, as people would surrender dollars more easily. Fundamentally, the degree of devaluation would depend upon the demand curve for real goods in suddenly uncertain dollars. If confidence is shaken just a bit, or people hold few dollars, then demand might be price elastic, and a small revaluation might lead to zero net redemptions. If confidence is shaken a lot, if people hold large stocks of dollars, if some shock creates inelastic demand for real goods ad services, then the devaluation (inflation) could be large. In ordinary times, the stock of money is mostly irrelevant, and in fact large stocks of unbacked money creates real benefits. But in extraordinary times, when the flow into money fails, the stock of outstanding money contributes to the likelihood that an inflation will be violent. (Unmodeled demographic changes, rather than investment losses, could also lead to net outflows and valuation crises.)
If a monetary authority has taxing power, could it overcome a shortfall of inflows of real goods and services relative to desired redemptions by taxing? Under our framework, that’d be a tricky thing to try to do. Taxing the money balances of the wealthy doesn’t much affect the flow of resources, except for agents who would have sufficient balances to cover idiosyncratic losses other than for the taxation. So taxing the very rich does nothing, except alter notional insurance balances, while taxing those with little savings does reduce some flows out of money by forcing people to bear losses as hits to consumption rather than drawdowns of money balances. The most effective form of taxation, however, would be to force the poor to exchange goods and services for money, and then surrender the money to the state. Tax receipts from the poor are all real — they cannot be satisfied by drawdowns of notional money balances, and they reduce the net imbalance between flows into money and redemptions very directly. In other words, taxes are effective at preventing a monetary crisis only to the degree the are regressive and harmful to growth. Taxes on rich people with large money balances are only effective if they are confiscatory, bringing those money balances to near zero.
What if we reimpose our “no systematic risk” assumption, so we don’t have to worry about shortfalls, but allow there to be more than one notionally risk-free asset? Then our Nash equilibrium becomes potentially unstable. So long as agents expect some net positive flow to all monetary assets, they are indifferent among them. But that indifference means that no barrier prevents agents from withdrawing claims from one monetary asset and exchanging it for another. If agent behavior is not random, if trends or “sunspots” might affect financial asset choices, and each agent would try to choose whatever asset they expect other agents would predominantly choose. There could be inexplicable runs to and from assets, similar to banks runs, except under our assumptions all agents already know that all monies are in some sense equally insolvent. Runs might be random (or based on unmodeled markers of “confidence”), unless and until only one survived.
Now let’s consider alternatives to the assumption that real goods and services exchanged for money are “thrown into the sea”. We won’t relax the deep (and important) assumption that aggregate wealth is not storable: it must continually reproduce itself via investment. So the monetary authority doesn’t have the option of simply holding the “stock” of goods and services it collects to back the stock of money. So what if, instead of throwing the stuff into the sea, the monetary authority just gives it away? Let’s consider two cases. First, suppose the monetary authority disburses the goods and services it receives to “poor” people. Under our assumptions that would be a Pareto improvement over ocean disposal. Aggregate growth is maximized, as in the perfect equality case (as all real resources would be continually reinvested until all agents reach their desired risky asset portfolio). Suppose the monetary authority transfers the real goods and services it receives back to the wealthy people who surrendered them? Under our assumptions, this sets up an endless loop. Wealthy people would rather have money than real goods and services, so they’d just sell the subsidy back for money. (Despite the apparent absurdity of this, wealthy people would prefer to receive transfers than have them go to the poor, as they gain insurance value from the notional money stock they build by continually receiving and selling back goods.) Transfers to wealthy people yield potentially unbounded growth in the stock of (still unbacked) financial assets, while transfers to those poor enough to invest in the real economy yield growth. Once the economy reaches its steady state, there are no growth-enhancing transfer possibilities left; all agents can maintain their desired level of real investment without transfers, and transfers just increase the notional money stock. Assuming that the monetary authority can’t invest on its own account, it has little to do with the stuff it receives other than to throw it into the sea.
Instead of making transfers, the monetary authority could lend the goods and services it receives from the rich to the poor. Under my assumptions, those sufficiently the poor would borrow and profitably invest if the interest rate charged is less than the expected return, and if resources are lent at the risk-free rate of zero, all those who hadn’t saturated their risky portfolio would be willing to borrow, and the growth rate could be maximized. This corresponds to people’s intuition about how a perfect or transparent financial system would behave. (Interestingly, if the monetary authority lends rather than transfers, growth might last a bit longer than in the perfect equality or transfers-to-the-poor cases, as agents would have to generate somewhat more than their own desired wealth, because some real wealth would continually belong to the monetary authority during the growth phase. Once the economy reaches the steady state, if the monetary authority cannot invest on its own account, the real wealth it holds is surplus and can no longer be reproduced, and so must be thrown into the sea.
If we imagine that the monetary authority can and does invest on its own account as well as private agents, then inequality doesn’t matter and the economy grows indefinitely at the rate of expected return on investment. If we imagine that the monetary authority can and does invest on its own account, and earns higher returns than economic agents, then inequality would be positive for aggregate growth. If we imagine that the monetary authority does things that yield no return but enhance private returns on investment (for example, creating public goods with the resources it purchases by issuing money), we can’t make any prediction about the effect of inequality without modeling the details.
Some observations: The true heart of this model is the idea that, beyond a certain level of wealth, people prefer the security of saving to expanding personal consumption. In real life, I think this is true of most, but not all, people. It’s a condition that I used to characterize, back in the optimistic 1990s, as “post-affluence” or “post-materialism”. In the steady state of this model, there is wealth inequality but consumption equality. The formerly rich are somewhat better insured than the formerly poor, and savvy investment choices can further increase agents’ degree of security (or position in status competitions), but people are satisfied with their level of consumption and don’t much alter it. Changes in consumption patterns result from changes in technology rather than idiosyncratic improvements in economic circumstance. I think this is a state of affairs worth thinking about. Again, in reality, people are not identical, both in terms of levels of consumption at which they’d be content and propensity to switch from consumption to savings at high levels of wealth. But in the 1990s, in my little bubble of opportunity-rich tech types, I did wonder whether we might become a “post-affluent” society, something like what the steady state of this model suggests.
One interesting characteristic of this model is that poor immigrants are good for aggregate growth. As the economy grows, agents become rich and content and cease contributing to growth. Importing poor people who are still striving creates growth and increases steady state GDP, but not GDP per capita (although one could posit indirect spillovers from aggregate growth to technological change, public goods provision, or somesuch). I think there’s something to that.
Some semi-technical miscellany
For simplicity, we’ve assumed (unrealistically) that all agents have identical preferences and opportunities. They only differ in their level of wealth. In the real world, peoples’ opportunities and risks vary. In the real world, there are a wide variety of financial assets, some financial asset purchases do affect real investment, and people choose to purchase financial assets rather than real assets in order to capture return, not just to hedge the risks of their own real lives. People may choose financial assets over real assets due to informational problems: high return projects may be available, but it may be difficult or costly to discover them. This model assumes all that away. Agents always know the return distribution they face for real investment; both risk and return are constant. In reality you’d expect diminishing marginal returns to risk (for any given search cost). These effects work in different directions: the fact that financial investment does affect growth-producing real investment by business and government means we are likely to overstate the cost of inequality in the model, but the model excludes many reasons for purchasing financial assets, so it potentially underestimates the scale of inefficient financial asset purchases.
We haven’t drawn a distinction between wealth and income inequality, because under the assumptions of our model, real income is always proportional to real wealth. However, perceived wealth includes monetary holdings. Under our assumptions, income eventually decreases as a proportion of perceived wealth, as agents invest in nonyielding money. In the steady state, there is perfect income equality, although the rank order of perceived wealth is preserved (in expectation) from the starting distribution.
We haven’t drawn a distinction between “consumption” and “investment”. If agents are rational and have time-consistent preferences, the distinction is immaterial: agents make purchasing decisions that yield a stream of consumption over time, and there’s no reason to treat the enabling of consumption at time zero any differently from consumption at time seven as long as the allocation is optimal. We concern ourselves only with “real expenditure”, and the returns thereon. Our intuitions about the distinction between consumption and investment have to do with lived knowledge that people’s preferences are not time-consistent, that it is hard to defer consumption however “rational” that might be. But even intuitively the distinction between consumption and investment is murky. Is eating consumption or investment? On the one hand, to eat is literally to consume. On the other hand, failing to eat reliably leads to reduced future returns on labor. Maybe some minimal “necessary eating” is investment, and the rest consumption? But we have a notion of poor investment for other goods. Why is it better to consider eating dessert “consumption” rather than superfluous and foolish investment?
I’ve been very vague throughout about the distinction between “financial assets” and “money”. That’s intentional but sloppy. Money is the purest example of a financial asset arguably backed by nothing, whose issuers (both governments and banks) may waste, lend, or transfer the real goods and services they receive in exchange for the funds they issue. But other financial assets may be similar, if people purchase them because they seem safer than forward-looking personal spending, and if net issuance results in transfers, loans, or manager perqs rather than direct productive investment. Financial assets whose issuance funds the purchase of real capital goods would count as risky investment rather than money in our model. I also need to think about how purchasing appreciated assets in secondary markets fits in: I think there should be something of an equivalence between assets like money whose increase in aggregate value takes the form of new issue under nominal price stability, and less supply-elastic financial assets which see price appreciation rather than new issue.



