Hedge funds and day traders are often claimed to provide liquidity to the markets they participate in. It’s clear that these actors do increase market turnover and reduce observable bid-ask spreads. But I contend that their participation may paradoxically increase the spreads paid by longer-term investors, who don’t buy and sell on a near instantaneous time-frame, but make portfolio adjustments infrequently and effect those adjustments over a period of time. How is this possible? Shouldn’t hedge-fund liquidity reduce trading costs for all participants?

In economics, “supply” and “demand” are defined not by numbers, but by curves. It is incoherent to ask “what is the supply of tennis balls”, and expect a number. The number of tennis balls the economy will produce, even in the short run, depends upon their price. We may ask “what is the supply of tennis balls, presuming they can be sold for $1 each?”, we’d get one number. If we ask, “what is the supply of tennis balls, if they can be sold for $10 each?”, we’d usually get a much larger number. Thus, though we may informally talk about “supply increasing”, that’s a more complicated idea than most people take it to be. The supply of tennis balls unambiguously increases only if at all prices, the quantity produced would be larger than at some earlier time. But, it is quite possible for a change to occur in an economy, whereby the number of tennis balls that would be produced for $100 increases, while the number that would be produced for $1 decreases. Has “supply” increased or decreased? Neither, exactly.

Similarly, I think that liquidity ought be defined not by any number (like a bid-ask spread, or “price impact” to immediate large trades, or length-of-time required to trade some volume within a constrained spread), but by a surface in a three dimensional space whose dimensions are spread, quantity, and time.

Suppose that we have an asset A, and we wish to define the liquidity of that asset in terms of some currency C. We will define spread as the minimal cost we can achieve buying and selling some quantity (defined in terms of C), within a preset period of time. For example, if I want to know the spread of associated with trading a specific natural gas future in dollars, I’d need to specify how many dollars worth of futures I’ll need to trade, and over what period of time I’m permitted to draw out my trades. We’ll say $1M dollars, over 3 days. Then I’ll ask an “optimal trader” (I know, that’s like a unicorn, but this is a thought experiment) to buy and sell $1M dollars worth of futures within a maximum of 3 days, at the end of which her position must be neutral. Our trader controls only the amount and time timing of the roundtrips. She does not control the order in which trades occur, and cannot force a delay between the two legs of the trade, so she cannot speculate on the underlying direction of the market.[1] Our trader is “optimal” in that she adopts the strategy that results in minimum loss, given her quantity requirement and time constraint. The total cost of this game, normalized to a per-dollar basis, defines the spread for natural gas futures as a function of quantity and time.

By reason alone, we know something about the way outcomes of this experiment will vary with different deadlines. As the deadlines get longer, the spread observed can not get larger. If our trader can recycle $1M through gas futures markets at a cost of $10K in 1 day, giving her two days can only help, since she is permitted to terminate early if that’s the optimal strategy. So, we are certain that spread as a function of time is strictly non-increasing.

No such mathematical certainty accompanies the relationship between spread and quantity traded. But, although one can contrive unusual cases, as an empirical matter, spread generally increases as a function of the amount that must be traded.

For any asset whose price fluctuates, the spread required by market-makers might vary with time, but should never quite go to zero. Each trade, however distant in the future, represents a sequential purchase and sale, which implies that some other party bears price risk for some interval. Risk-averse market-makers will always require some compensation for bearing risk. Assuming that their level of risk-aversion does not change (including any capacity to hedge), their compensation requirement should increase with their degree of uncertainty about future prices, and the length of time they expect on average to hold positions. The non-zero compensation requirement of the least risk-averse, most certain, lowest-transaction-cost market-makers who ever occasionally transact should define an asymptotic lower bound to spread with increasing time.

Given all this description, we can now draw a qualitative picture of a liquidity:

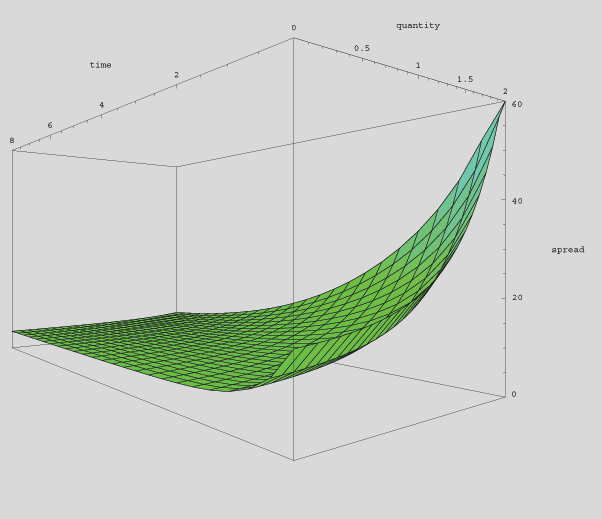
(The units here are arbitrary.)

Now let’s consider what happens to a liquidity surface when a new population of “noise traders” enters the fray. We’ll assume they have to following characteristics:

1. They are frequent traders, as a group always willing to buy and sell at some price.

2. They are not particularly risk averse. The compensation they require for bearing risk-of-ownership is less than that participants in the market had typically obtained prior to their entry.

3. They are reasonably efficient transactors. The transaction costs they face are similar to those faced by other active market participants.

4. Much of their valuation process is “technical” (market price and momentum-based) and game-theoretical rather than “fundamental” (based on analysis of cash-flows achievable from holding the underlying independent of market activity).

How does the entry of this population into a market change the spread achievable on a short time frame, that is when a trader must transact within a short period of time from a randomly chosen moment? Property 1 implies that this population is likely to be active at an arbitrarily chosen moment. Properties 2 and 3 imply that newcomers are likely to be willing to compete with previously existing market-makers, driving down observed instantaneous bid-ask spreads.

But how does this new group affect the spread observed by patient traders, who are in no rush, but wait for the most opportune time to conduct their transactions? There is no certain answer to this question. Recall that as the time horizon goes to infinity, the spread is determined by the lowest-spread market-makers who ever buy or sell, no matter how infrequently. If the new participants, either by accepting less compensation directly or by increasing competitive pressure, reduce the spread required even by the most inexpensive occasional market-makers, then the entry of the new traders will diminish spreads even at long time horizons, implying an unambiguous increase in liquidity.

But suppose that that the previous low-spread market makers achieved their price advantage not by virtue of high risk-tolerance or low transaction costs, but by superior skill at valuing the underlying asset. If the trading habits of the new market participants (see Property 4 above) leads to an increase in unpredictable price volatility, then their entry into the market may diminish those participants’ prior ability to predict future prices. In this case, the entry of the new participants will simultaneously reduce spreads at low time horizons, while increasing spreads paid by more patient players. This situation is depicted below. The green surface depicts the liquidity of the market prior to the entry of “noise traders”. The red surface shows what happens when “noise traders” enter the market, a simultaneous raising and flattening of the liquidity surface.

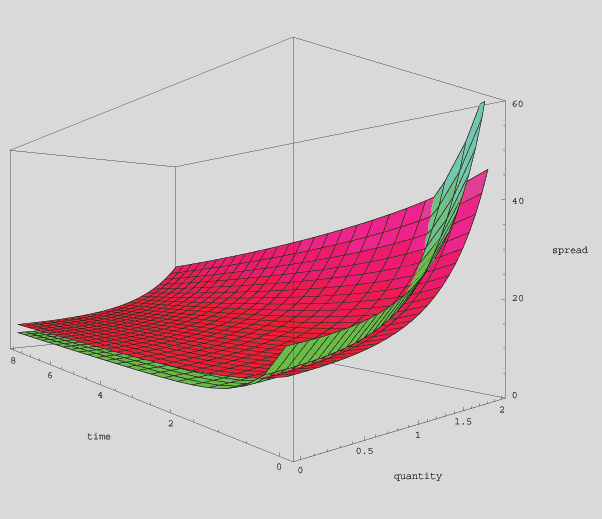
Over a short time horizon, the new (red) surface offers lower spreads than the original (green) no-noise-trading surface. (The green “lip” at the front of the graph indicates higher spreads for the original surface than for the red noise-trading surface.) Bid-ask spreads visible in limit order books will generally show lower spreads when noise-traders are present than when they are not. But buyers or sellers willing to spread out moves over a prolonged period will find that the best achievable spreads are worse when noise traders are around than it would have been prior to their entry. Thus, a paradoxical sort of liquidity (or illiquidity) is provided by noise-traders: They reduce costs for traders with short time-horizons who demand quick trades. But they increase trading costs paid by longer-term investors.

Is defining liquidity of an asset as surfaces like this novel? If any readers know of similar definitions, or other approaches to characterizing liquidity (besides mere instantaneous spread or volume measures), please do let me know. I’d thank commenter moldbug; this idea came out of his pushing me to define things in a very thoughtful comment debate.

I don’t really want to be writing about this now. I had hoped to spend today theorizing obscurely about liquidity. But, after reading (via Felix Salmon) the apologetics of a bunch of prominent economists for inequality (here, here, and especially here — or here via Mark Thoma, to get around Times Select), I just have to go off half-cocked a bit.

Earth to Economics Professors! Earth to Economics Professors! In this, the real world that we inhabit, There Is No Such Thing As A Pareto Improvement. An increase in inequality (or an increase in equality for that matter) always helps some people and hurts others in a variety of ways. Period.

You can claim, if you like, that the harms people experience by increased inequality are outweighed by other benefits, even to the harmed. But the dimensions along which people are harmed and helped are incommensurable. Conventional economic simplifications like “real income” do not capture the full effect of the changes. And we need not and should not, resort to emotional fairy tales like “spite and envy” (as in a previous blogospheric inequality controversy) or “inequality of happiness” (an unfortunate addition today by the usually excellent Tyler Cowen).

Increases in wealth to the wealthy can harm the less wealthy in many ways that don’t show up in “real income” stats. Here are two important but often overlooked examples:

1) Inaccessibility of public goods for which superior private substitutes can be purchased

Consider almost anything that is arguably a “public good” — parks, well-paved roads, transportation in general, schools, medical care, social insurance, personal security. Private substitutes are available for nearly all of these goods, to those who are sufficiently wealthy. Who needs a park, when one can buy a home with a lovely back yard? Is it worth paying high taxes to keep the roads smooth, when one can purchase an SUV, or a helicopter, that is not bothered by potholes, and is more comfortable and functional than an economy car anyway? Speaking of cars, should we just invest in an excellent streetcar and/or subway system, and not spend so much money on roads? Should we accede to higher taxes to support well appointed public schools, or do we prefer strictly private education? Should I support taxes to fund the police, when in any case I am going to require expensive private security?

Rational individuals will answer these sorts of questions very differently, depending on their circumstances. To those for whom the marginal utility of a dollar is low, buying superior private substitutes for public goods will appear to worthwhile. They will oppose government purchase of these goods and the taxation required to support it. But, poorer people will find the dollar cost of private substitutes to be burdensome, and will rationally choose less expensive state provision via inferior public goods. Choices have to be made. We build a comprehensive subway system, or we don’t; we buy and maintain a new park, or we don’t; we tax to fund more policing, or we don’t. Increases in inequality (particularly increases in the numbers and the political influence of the relatively wealthy) shift the likelihood that we opt for private provision of what could be provided in an inferior manner, but at lower cost-per-person, as a public good. Poorer people are forced to pay more for a service than they would have under the policy they would have chosen, or to do entirely without services that might have been provided them inexpensively by the state.

2) Goods and services become expensive, or fail to be produced at all, under inequality, due to reduced economies of scale and increased resource prices.

The mix of goods and services produced by a society is affected by the distribution of wealth in that society. It is easy to see that luxury goods might fail to be produced in very equal societies. Suppose, counterfactually, that we could have an economy in which goods and services are produced as efficiently as they are currently, but with no inequalities in wealth or income, everyone earns the same, current US-average income. The market for Lamborghinis would dry right up. But the converse holds as well. Suppose that the same society is divided into two groups, one wealthy enough such that the superior performance of a Lamborghini is clearly worth the extra expense, and another group whose wealth is roughly the current US-average. The poorer group will be adversely affected by the sudden good fortune of their neighbors. As the market for economy cars will be cut in half, economies to scale in auto production will be adversely affected. Car companies might be the first to take a hit, as they will have already sunk costs based on now violated scale expectations. But new lines of economy cars will have to be designed more sparely, or else priced more expensively, in order for car companies to build profitable econoboxes. The scale effect is exacerbated if, plausibly, Lamborghini production utilizes more non-human resources (metal, energy, etc.) than econobox production. Goods prices will be bid up by the wealthy half of the world, and price and quality of the econoboxes will thereby suffer as well. There may be dynamic effects that mitigate the ill effects of half the world’s sudden good fortune on the other half, but even in this most contrived case, you can’t claim a simple “Pareto improvement”.

The above is not to suggest that inequality is inherently bad. On the contrary, my intuition is that most societies I’d want to live in would tolerate a great deal of inequality. But “a great deal” does not mean unlimited, and tolerance does not imply unconditional cheerleading. At this moment in the United States (and throughout the world), a lot of people (myself included) see a disturbing degree of inequality whose growth, we believe, is insufficiently attached to the kind of positive effects that sometimes persuades us that inequality is a good thing. We may be mistaken. But today’s crop of justifications, by authors whom I usually admire, struck me as shallow, glib, and unserious.

Tim Iacono very aptly titles a post about the much-discussed “liquidity” in world markets, Hard to Define and Measure. I have long thought the notion of liquidity was ill-defined and under-theorized. Never fear, because, as usual, I have the answer!

In loose talk, liquidity usually has something to do with the quantity or availability of money. From this perspective, liquidity means a high monetary base, low interest rates, and/or easy access to credit for prospective borrowers. The academic literature usually operationalizes liquidity in terms of the bid-ask spread and price impact. In a liquid market, the bid-ask spread is narrow, and price-impact small. (Price impact refers to the amount prices change disadvantageously when one attempts to buy or sell a commodity.)

My proposal is that liquidity should be defined very simply as certainty of valuation of an asset with reference to some currency or commodity. An asset whose value in dollar terms is 100% certain is perfectly liquid in dollars. An asset whose value is completely random or unknown would be perfectly illiquid in dollars.

This definition maps very nicely to the academic stand-ins for liquidity. One needs only assume the usual no arbitrage condition to see this. Suppose there were a market (in dollars) for $10 bills. The dollar value of a $10 is trivially certain. What would the bid-ask spread be in this market? If a market maker could consistently sell ten dollar bills for $10.001 or buy ten dollar bills for $9.999, the market-maker could make infinite, risk free profit by doing so in volume. The bid-ask spread on $10 bills must quickly converge to zero to prevent a tear in the fabric of the financial universe. Similarly, suppose I have a zillion $10 bills to sell. Will the price move against me? In a world without informational frictions or transaction costs, no. If some market shyster, seeing that I’m desperate to sell, offers only $9.999 a piece, some other entrepreneur, eying a perfect arbitrage, will quickly offer $9.9995, until the price converges to $10 nearly instantaneously. You can see all of this in action in the real world. If you ask to “sell” a ten-spot (that is to make change) most store owners will buy it for you for precisely 10 one dollar bills. If you have a hundred thousand tens, a bank will purchase that truck-load for one million dollars. (This sort of purchase is called a “deposit”.)

The relationship between an informational definition of liquidity and the popular notion of “lots of money sloshing around” is more subtle, but very much worth teasing out. In addition to requiring the no arbitrage condition, we’ll make two additional assumptions. We’ll presume that as the quantity of a currency increases, so too do transaction volumes in that currency. (This is equivalent to the conventional monetarist assumption that money velocity is resistant to change.) We’ll also presume that market transaction prices vary continuously, and that the rate at which prices change over short periods of time is bounded and not sensitive to changes in the quantity of money. Under these assumptions, an increase in the availability of money also leads to an increase in informational liquidity. Why? Because given a current price, a prospective buyer or seller of an asset is fairly certain as to a near-future realizable price, since transactions are frequent and the rate at which prices change is bounded. A current price represents a fairly certain near future value in the currency at issue. From an informational perspective, it’s not the extra money that represents the liquidity, but the frequent, near-continuous transactions provoked by the ready availability of the currency. I like to think of the sort of liquidity caused by extra money as “sample rate liquidity”, in that it decreases the uncertainty of valuation by increasing the sample rate of the fluctuating values.

I think that an information definition of liquidity can be made precise, and that many fruitful avenues for research that could be derived from it. If one assumes that markets are efficient, and that market prices reflect but do not alter the value of underlying assets, one can consider transactions to be samples of a noisy signal. Each trade price represents a sample, and the size of the trade is a measure of sample accuracy. From signal theory we know that for any signal whose maximum frequency in the Fourier transform is bounded, there is a sample rate that is sufficient to reconstruct the signal perfectly, such that further sampling would be pointless. If one views financial markets as decision-making institutions, devices whereby economies tease out information about the true value of potential enterprises and investors then devote scarce resources to the most useful, then a bound on the liquidity required to fully value an asset over time represents a bound on useful liquidity. If one also presumes the existence of “noise traders”, entities who engage in transactions for reasons detached from a valuation of the asset being traded, and presumes that noise trading is sensitive to money availability, a bound on informationally useful liquidity should become a normative bound to central banks or other currency issuers, as increases in the availability of a currency beyond this bound increases noise without contributing to asset valuation, increasing the likelihood that an economy will devote scarce resources to erroneously valued projects. Similarly, insufficient “sampling rate liquidity” could lead to “aliasing”, where the underlying signal and its sampled reconstruction may bear little resemblence to one another. Between aliasing and noise-trading, there should be an informationally optimal level of “sample rate liquidity”, and potentially an informationally optimal level of money and credit for a given stock of tradable assets and a maximum frequency of “real” value fluctuations.

There is much more to go from here. Suppose, counter to our assumption above, the rate at which prices fluctuate is in fact sensitive to the quantity of money and credit availabilty. Then conventional measures of liquidity, like the bid-ask spread, might either expand or decline in response to increased money, depending on a race between the increased slope of the price time-series and the increase in the frequency of transactions. In either case, this is a bad situation, as increased market activity, rather than more precisely valuing resources is simply decreasing the precision which with resources can be valued. I think a real world analysis would show that the effect of money and credit are non-uniform, that there are times and circumstances where additional money is likely to improve the informational resolution of markets, and times when it is likely to magnify noise, and that with a bit of effort, theoretical and empirical, these regions could be usefully characterized. I don’t think Taylor-rule-style monetary regimes even begin to capture this dynamic. Readers of this blog will be unsurprised to know that I think we are presently in a region wherein “lots-of-money-sloshing-around” is creating the appearance of liquidity (narrower spreads, less price impact) without the sine qua non of genuine liquidity: additional information or certainty about the real-economic value of the assets being exchanged and priced.

Dick Cheney may disagree, but most people think of large, structural government deficits as a bad thing. Sure, a case can be made for temporary, stimulative deficits, but “over the cycle”, a government’s books should be close to balanced. Right?

Maybe not. When a country’s currency is held artificially strong by mercantilistic trading partners, perhaps the best countermove is for governments to invest in future tradables capacity by borrowing aggressively to purchase underpriced foreign goods.

Suppose mercantilistic nations subsidize exports to a country by keeping their currencies artificially cheap relative to that of the target country. Then, for a period of time, production of tradables in the target country becomes uncompetitive. Labor and capital are redirected to nontradable sectors of the economy, a current account deficit develops, and the domestic cost of capital is depressed by foreign central bank interventions. This state of affairs cannot be expected to persist forever, as currency intervention is costly to the intervening countries. (But it can persist for a long time, because the costs of intervention may be hidden and widely dispersed.) When the intervention ceases, the target of the currency manipulation will have to revive its tradables sector.

A rational response by the country whose currency is being propped up would be to devote the subsidy it receives (in the form of exaggerated buying power and cheap capital) to easing an expected future adjustment back into tradables production. But the difficulty of a reorientation to tradables is likely to increase with the length of time the tradable sector is kept artificially uncompetitive. So, an optimal policy would try to simultaneously maximize the total subsidy received, minimize the time over which it is received, and ensure that a sufficient portion of the subsidy is devoted to enhancing future tradables production.

One plausible response would be to try to maximize the rate of consumption of subsidized imports by domestic consumers. A sufficiently high rate of domestic consumption could achieve the first two goals: maximize the subsidy and minimize the time over which an adversary’s intervention is sustainable. But there are many problems with this approach. First, consumption expenditures, taken as a whole, are unlikely to represent effective investment in future tradables capacity. Second, it is hard to see how a country could encourage consumption at levels higher than those desired by the intervening countries. Should a government start an advertising campaign encouraging the citizens to buy more of some particular foreign country’s products? Finally, sufficiently high levels of expenditure might require many consumers to take on a great deal of debt, which they may be reluctant to do, or if they are not reluctant, may have future adverse consequences for the domestic economy.

A better response would be for the targeted country to borrow at the artificially depressed rates, and then invest the proceeds in some manner designed to enhance future domestic tradables production. For this to work, the targeted country would have to make real investments, especially by purchasing underpriced tradables, not merely save the proceeds as financial assets. (Think about it.) This borrowing and investing could be accomplished by either the private sector or the public sector of the targeted country. But, although the private sector might be eager to take on leverage in order to extract the subsidy of low interest rates, it is ill-equipped to invest the proceeds in future tradables capacity during a period when, for the foreseeable future, domestic tradables investment is expected to underform foreign tradable or domestic nontradable investments, dramatically. Also, a dramatic increase in private sector debt increases financial risk, both to the entities that take on leverage directly, and to the financial system as a whole, in ways that may not be desirable. Finally, as the ability to take on debt and profitably invest it is skewed towards the already wealthy, using the private sector to extract the foreign currency manipulation subsidy permits a foreign power to exacerbate domestic inequality, which may not be desirable.

The public sector, on the other hand, can borrow and spend at whatever level it calculates would best balance maximizing the current subsidy and minimizing the duration of other nations’ interventions. The public sector is uniquely capable of making not-profit-maximizing investments on a large scale, and may wisely do so when such investment represents a “public good”. Debt taken on by the public sector in its own currency can in the worst case be monetized. A sharp repricing of the currency spurred by monetization is a no-brainer when sufficiently large quantities of debt, public or private, are owed to foreigners. Mere consideration of aggressive, intentional deficit expansion to extract a currency manipulation subsidy would likely spook many private holders of domestic currency, increasing the cost and difficulty for currency interventions, and perhaps even ending them before a dime of extra public debt is actually assumed.

What would a program of massive government borrowing to invest in future tradables capacity actually look like? Well, it would be the mother of all pork programs. It would involve massive infrastructure spending; constructing well-appointed, transportation-linked industrial parks that private developers would not build on their own; fiber-lit India-style “campuses” for hosting tradable service organizations; increased capital spending on science; maybe a public organization devoted to retaining skills and knowledge in industries that have moved offshore, in case they need to move onshore again someday. Of course, many of these projects would amount to malinvestment and overcapacity, but still public sunk costs would provide private opportunities for manufacturers able to rent wonderful facilities dirt cheap. Retrospectively, these errors would function as, well, subsidies to domestic tradables producers. But prospectively, each project would have been undertaken as wise investments in the public interest, so no trade rules would be violated. The investment program wouldn’t need to be perfect. It would have to be large enough to create costs for currency interveners, and should ensure that more of the currency intervention subsidy goes towards future domestic tradables production than would happen without the program. The very real dangers are that corruption and cronyism in government spending might transform capital investment programs into redistribution of consumption programs, or that corrupt or indisciplined public buyers would pay overmarket prices for tradable capital goods, subsidizing rather than creating costs for currency manipulators.

Many readers, I suspect, will be perplexed by the notion that government deficit spending explicitly to purchase more goods from a mercantilistic currency manipulator could be a strategy for ending that manipulation and eventually for bringing currant accounts into balance. Doesn’t a government deficit contribute to a current account deficit? Isn’t selling more goods exactly what currency manipulators are trying to accomplish by underpricing their currencies? Well, yes. But as any wrestler knows, sometimes you can throw an adversary off balance more effectively by moving too quickly in the direction you are being prodded to move than by putting up a well-anticipated fight.

Suppose a government were to borrow funds to buy up enormous quantities of steel, cement, rail, industrial machinery, or other merchanidise the production of which is dominated by mercantilistic currency manipulators. The purchasing government gets a good deal, as both the interest-rates it pays are below-market and the price it pays for goods is cheap due to the producers undervalued currencies. However, the massive purchases create inflationary pressures for the currency manipulators, twice. The price of the goods they sell (and use internally) is bid up by the sudden increase in demand. And the central banks of the manipulating countries have to buy up the extra inbound FX, in order to maintain their floors for the targeted currency. Buying the inbound currency requires expanding the domestic money supply, which contributes to domestic inflation. The central bank can fight inflation by raising interest rates or issuing sterilization bonds, but both strategies are costly. Also, as the price of some commodities is held high by sustained demand and limited capacity, fighting inflation implies accepting disruptive deflations in the price of other commodities. The currency manipulator can either acquiesce to the inflation (acquiescing to real appreciation), double down by trying to increase capacity, or cry uncle, give up the nominal peg, and let currency fluctuations and a spike in interest rates price the aggressively purchasing government out of the market. Increasing capacity is hard, slow, and counterproductive. (Just as the economy targeted by the currency manipulator faces a future adjustment into tradables production, the currency manipulator itself knows it will eventually need to rebalance out of a tradables-skewed economy.) The only way that a currency-manipulator can avoid taking losses to an overly aggressive buyer is to raise the price to the buyer of the goods it sells, by abandoning (in real or nominal terms) the floor it has tried to plant beneath the targeted country’s currency.