Liquidity Surfaces and Hedge Funds
Hedge funds and day traders are often claimed to provide liquidity to the markets they participate in. It’s clear that these actors do increase market turnover and reduce observable bid-ask spreads. But I contend that their participation may paradoxically increase the spreads paid by longer-term investors, who don’t buy and sell on a near instantaneous time-frame, but make portfolio adjustments infrequently and effect those adjustments over a period of time. How is this possible? Shouldn’t hedge-fund liquidity reduce trading costs for all participants?
In economics, “supply” and “demand” are defined not by numbers, but by curves. It is incoherent to ask “what is the supply of tennis balls”, and expect a number. The number of tennis balls the economy will produce, even in the short run, depends upon their price. We may ask “what is the supply of tennis balls, presuming they can be sold for $1 each?”, we’d get one number. If we ask, “what is the supply of tennis balls, if they can be sold for $10 each?”, we’d usually get a much larger number. Thus, though we may informally talk about “supply increasing”, that’s a more complicated idea than most people take it to be. The supply of tennis balls unambiguously increases only if at all prices, the quantity produced would be larger than at some earlier time. But, it is quite possible for a change to occur in an economy, whereby the number of tennis balls that would be produced for $100 increases, while the number that would be produced for $1 decreases. Has “supply” increased or decreased? Neither, exactly.
Similarly, I think that liquidity ought be defined not by any number (like a bid-ask spread, or “price impact” to immediate large trades, or length-of-time required to trade some volume within a constrained spread), but by a surface in a three dimensional space whose dimensions are spread, quantity, and time.
Suppose that we have an asset A, and we wish to define the liquidity of that asset in terms of some currency C. We will define spread as the minimal cost we can achieve buying and selling some quantity (defined in terms of C), within a preset period of time. For example, if I want to know the spread of associated with trading a specific natural gas future in dollars, I’d need to specify how many dollars worth of futures I’ll need to trade, and over what period of time I’m permitted to draw out my trades. We’ll say $1M dollars, over 3 days. Then I’ll ask an “optimal trader” (I know, that’s like a unicorn, but this is a thought experiment) to buy and sell $1M dollars worth of futures within a maximum of 3 days, at the end of which her position must be neutral. Our trader controls only the amount and time timing of the roundtrips. She does not control the order in which trades occur, and cannot force a delay between the two legs of the trade, so she cannot speculate on the underlying direction of the market.[1] Our trader is “optimal” in that she adopts the strategy that results in minimum loss, given her quantity requirement and time constraint. The total cost of this game, normalized to a per-dollar basis, defines the spread for natural gas futures as a function of quantity and time.
By reason alone, we know something about the way outcomes of this experiment will vary with different deadlines. As the deadlines get longer, the spread observed can not get larger. If our trader can recycle $1M through gas futures markets at a cost of $10K in 1 day, giving her two days can only help, since she is permitted to terminate early if that’s the optimal strategy. So, we are certain that spread as a function of time is strictly non-increasing.
No such mathematical certainty accompanies the relationship between spread and quantity traded. But, although one can contrive unusual cases, as an empirical matter, spread generally increases as a function of the amount that must be traded.
For any asset whose price fluctuates, the spread required by market-makers might vary with time, but should never quite go to zero. Each trade, however distant in the future, represents a sequential purchase and sale, which implies that some other party bears price risk for some interval. Risk-averse market-makers will always require some compensation for bearing risk. Assuming that their level of risk-aversion does not change (including any capacity to hedge), their compensation requirement should increase with their degree of uncertainty about future prices, and the length of time they expect on average to hold positions. The non-zero compensation requirement of the least risk-averse, most certain, lowest-transaction-cost market-makers who ever occasionally transact should define an asymptotic lower bound to spread with increasing time.
Given all this description, we can now draw a qualitative picture of a liquidity:
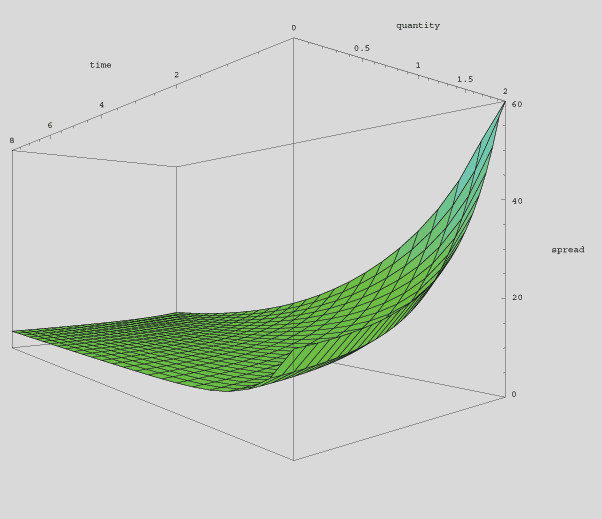
(The units here are arbitrary.)
Now let’s consider what happens to a liquidity surface when a new population of “noise traders” enters the fray. We’ll assume they have to following characteristics:
They are frequent traders, as a group always willing to buy and sell at some price.
They are not particularly risk averse. The compensation they require for bearing risk-of-ownership is less than that participants in the market had typically obtained prior to their entry.
They are reasonably efficient transactors. The transaction costs they face are similar to those faced by other active market participants.
Much of their valuation process is “technical” (market price and momentum-based) and game-theoretical rather than “fundamental” (based on analysis of cash-flows achievable from holding the underlying independent of market activity).
How does the entry of this population into a market change the spread achievable on a short time frame, that is when a trader must transact within a short period of time from a randomly chosen moment? Property 1 implies that this population is likely to be active at an arbitrarily chosen moment. Properties 2 and 3 imply that newcomers are likely to be willing to compete with previously existing market-makers, driving down observed instantaneous bid-ask spreads.
But how does this new group affect the spread observed by patient traders, who are in no rush, but wait for the most opportune time to conduct their transactions? There is no certain answer to this question. Recall that as the time horizon goes to infinity, the spread is determined by the lowest-spread market-makers who ever buy or sell, no matter how infrequently. If the new participants, either by accepting less compensation directly or by increasing competitive pressure, reduce the spread required even by the most inexpensive occasional market-makers, then the entry of the new traders will diminish spreads even at long time horizons, implying an unambiguous increase in liquidity.
But suppose that that the previous low-spread market makers achieved their price advantage not by virtue of high risk-tolerance or low transaction costs, but by superior skill at valuing the underlying asset. If the trading habits of the new market participants (see Property 4 above) leads to an increase in unpredictable price volatility, then their entry into the market may diminish those participants’ prior ability to predict future prices. In this case, the entry of the new participants will simultaneously reduce spreads at low time horizons, while increasing spreads paid by more patient players. This situation is depicted below. The green surface depicts the liquidity of the market prior to the entry of “noise traders”. The red surface shows what happens when “noise traders” enter the market, a simultaneous raising and flattening of the liquidity surface.
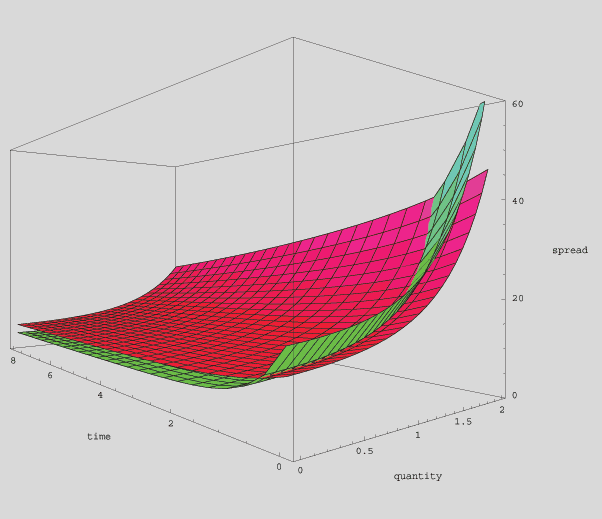
Over a short time horizon, the new (red) surface offers lower spreads than the original (green) no-noise-trading surface. (The green “lip” at the front of the graph indicates higher spreads for the original surface than for the red noise-trading surface.) Bid-ask spreads visible in limit order books will generally show lower spreads when noise-traders are present than when they are not. But buyers or sellers willing to spread out moves over a prolonged period will find that the best achievable spreads are worse when noise traders are around than it would have been prior to their entry. Thus, a paradoxical sort of liquidity (or illiquidity) is provided by noise-traders: They reduce costs for traders with short time-horizons who demand quick trades. But they increase trading costs paid by longer-term investors.
Is defining liquidity of an asset as surfaces like this novel? If any readers know of similar definitions, or other approaches to characterizing liquidity (besides mere instantaneous spread or volume measures), please do let me know. I’d thank commenter moldbug; this idea came out of his pushing me to define things in a very thoughtful comment debate.
[1] Our trader says when and how much; a coin is flipped and an order goes either to the buy or sell desk; once the first leg is fulfilled, an order goes immediately to the opposite desk to liquidate the position; the dollar value of the fist leg is added to a total-traded tally; the dollar cost of the round trip is added into the spread.

Interesting – thx.
January 29th, 2007 at 8:17 am PST
link
noise traders:”But they increase trading costs paid by longer-term investors.”
questionable claim,no noise trader => no liquidity.noise traders are on balance net losers and therefore subsidize information traders whether with long or short term horizons.
see:
noise by fischer black
http://powerswings.com/wp-documents/BLACK_1986.pdf
see also best book on the subject :trading and exchanges larry harris
January 29th, 2007 at 8:52 am PST
link
jck — First, thanks for the knowledgeable comment. I agree it’s a questionable claim that “noise trading” increases liquidity, and am aware of the argument that the existence of noise trading just creates a subsidy for information traders. But we have to distinguish between total profitability of investments and the costs faced by participants once they have chosen to buy or sell. The post makes claims about the latter, not the former. I have to disagree strongly with the statement “no noise trader => no liquidity”. I don’t think that’s right at all.
There’s a lot to untangle here. First we must define what we are talking about. This blog post does not try to suggest (though I might in other contexts) that noise-trading overall diminishes the profitability of information trading. It does claim that noise trading might reduce liquidity, in the sense of increasing transaction costs, to information traders with long time-frames who prolong execution to minimize transaction costs. Most observers (including Black in the paper) buy the notion that there is price, and there is value, and that price is a noisy reflection of a much lower frequency value curve. If one further posits that noise is unbiased (or that its biases are symmetrical, randomly distributed, and unguessable), then long-horizon traders ought to play-out large trades over time to minimize spreads paid. The strategy is risky — in any one instance, noise could move against one and drive up transaction costs — but by weak-unbiasedness, over multiple rounds, the strategy should be profitable so long as the length of the trades is short relative to the fluctuation in underlying value (though it may be long relative to noisy price fluctuations of the market).
Information traders may simultaneously benefit from noise traders by having price-mismatches-from-value to buy and sell, but lose because of increased transaction costs introduced by noise traders. Suppose momentum-trading hedge funds drive the price of a security above any reasonable valuation. It’s possible that an “information trader” despite cherry-picking over time to minimize, faces a larger spread in his short-sale then he would absent the noise-traders, but that the short sale turns out to be very profitable. This post only address the worsened “best spread”, not the profitable eventual round-trip.
Let’s come back to “no noise trader => no liquidity”. There would be no liquidity only under the dry and untenable assumptions of portfolio theory: perfect information, nearly identical agents who differ only in risk tolerance. If we posit irreducible uncertainty about the value of an asset, if we accept that different agents have different models and information that can’t be uniquely ordered into “better” or “worse” than that of other agents, if we allow that people have very different utility functions with respect to assets and currencies, and that those utility functions that change with time, there should be many opportunities to trade absent noise-traders. However, there is the potential that these “rational, informational” traders will suffer timing problems — when one wants to trade, no counterparty will be found. You imply, as does Black, that the only way to overcome this is to have noise-traders fill in the gaps. But this is overly pessimistic, I think. It ignores the possibility, and reality, that professional, rational market-makers would find a profitable niche. Given the varying information, varying utility functions based on that information, each trader perceives the trades they would engage in as positive utility. But some trades will fail to occur because of the inability of traders to agree on the time of trade. Rational traders would sacrifice some of the expected utility of a trade to pay someone to bridge that gap. A seller pays a market-maker (half a spread, by convention) to buy earlier than a natural buyer is ready to; a buyer pays a market-maker to hold-for-sale a security that would not otherwise be available. Market-makers are not noise traders; they are service-providers, compensated by traders for the risk they bear, and they make money in the real world. This should only be a surprise to the most dogmatic adherents of efficient markets, perfect information, and uniform agents. Noise-traders increase the risk that market-makers have to bear; market-makers therefore increase their prices.
That’s enough for now. There is still the question, putting aside distinctions between transaction costs and overall profitability as you did in your comment, do noise-traders increase or decrease net profitability to information traders? I think that the standard story, “Noise traders are a subsidy,” is at best overly simplistic and at worst wrong. If noise-traders are defined as entirely random actors, then I’ll concede that better informed traders can craft strategies that will profit from their behavior. But if noise-traders are defined to include “technical traders” and game-theoretic players (who base trades on hypotheses or information about other players holdings and likely actions), that is if we define as noise traders anyone other than those trading based on fundamental valuation of securities, then I think that that in many markets, “noise traders” may well turn the tables, and extract a subsidy from the quaint, naive information traders. I suppose the google keyword here is “limits to arbitrage”. But that’s for another time.
Thanks, jck, for comment, and for Alea, which is a wonderful resource.
January 29th, 2007 at 2:18 pm PST
link
Steve — It seems to me that your whole thesis rests precariously on one counterfactual:
Which I”m far from convinced is actually the case. Given that the increase in hedge-fund AUM has coincided quite cleanly with the decrease in observed volatility, what makes you think that in point of fact the new market participants actually increase vols at the margin? I think any empirical study would have a hard time demonstrating this.
January 29th, 2007 at 2:32 pm PST
link
Felix — That’s a fair criticism. You’ll note that prior to the conditional you highlight, I did duly acknowledge the other possibility (that as the new players enter a market, their presumed low risk tolerance and competitive transaction costs lead to a drop the liquidity surface along all time horizons, amounting to a clear increase in liquity).
There are two ways I’d respond:
First, though I did a poor job of emphasizing it, my primary thesis here was not that hedge funds, today, are in fact reducing liquidity for long time-frame traders. The main point, the reason for inventing “liquidity surfaces”, was to demonstrate that it’s conceivable for such a thing to happen, that commonly measured scalar stand-ins for liquidity (like observed instantaneous spreads and turnover) don’t adequately capture asset liquidity. It is possible for spreads to decline, as an average of instantaneous samples, while at the same time to increase as an actual cost for an important class of traders.
But, I’d not have given the post the provocative title and first paragraph
if I were not a publicity whoreif I didn’t think the idea had some relevance to present market controversies. A more practical rejoinder would poke at the definition of “the decrease in observed volatility”. In which markets, observed how? There certainly is a general meme that volatility is decreasing, and there are market oddities like the VIX, which seems to be suggesting 2:1 odds that the S&P 500 should not vary by more than ~10% per year, after it has just varied by nearly 18%, and when any measure of investor sentiment would, I bet, guess at more peak-to-trough variability than options markets are predicting (not arbitrageable, though, because VIX is extrapolated from short options, and the timing of the predicted excess volatility in uncertain).I think you’re right, though, that w.r.t. say the S&P 500, I’d have a hard time showing a diminishment of liquidity even “late” on the liquidity surface. US public equity markets have long had a wide variety of non-fundamental traders; I think hedge-fund activity, to the degree it plays in these markets, adds more to competition than to noise within most market-makers’ time frames. (Plus, public equity hedge-funds often like long/short strategies, which are the essence of “not-noise-trading”.)
I do think that if we were to choose a market that was previously esoterically traded primarily by knowledgeable participants, but that has recently become popular among hedge-fund investors, we could observe the dynamic I describe (compressed instantaneous spreads, worse real transaction costs for long-term patient traders). But I certainly haven’t done a study.
The proposition is not untestable, though. So long as records are kept of of market-maker quotes, we can compare not average but minimum spreads between the time periods. My hypothesis suggests that average spreads would narrow, but minimum spreads would widen.
I also should clarify something w.r.t. the quote you pulled out. Rather than “unpredictable price volatility”, perhaps I should have written “market-maker uncertainty”. Even if the empirical up-to-now volatility of a price series is quite low, and even if options markets (themselves inhabited by “noise traders”) are not predicting much volatility (that is, people are very comfortable writing options), it’s possible that professionals rather than noise-traders are the least-cost market-makers, and that professionals require a premium because they perceive an increased likelihood of sudden, long-tail events. We really can’t use volatility measures as a stand-in for expected spread. We have to observe what market-makers are actually requiring as compensation. Fortunately, spread minimums are observable. They just aren’t what people usually measure.
January 29th, 2007 at 3:56 pm PST
link
[btw, if we’re considering an empirical study, we have to pay attention to minimum spreads restricted by quantity, realizable throughput. Minimum spreads go to zero as the quantity and/or pace of trading go to zero.]
January 29th, 2007 at 4:27 pm PST
link
Steve,
“Minimum spreads go to zero as the quantity and/or pace of trading go to zero”
good point
we have to remember that one of the reason bid/ask spreads have been shrinking is because of the increased “speed of finance”.
a thin spread good for 60 milliseconds can only provide liquidity for a very small volume of trades.even if the “wholesale” spread is the same than before there is a net gain for a longer term traders because they can pick up crumbs between the boundaries of the “wholesale” spread.what this does is force traders to slice and dice their orders to try tp pick up the crumbs hence the huge increase in algorithmic trading.so we have a kind of vicious circle[or virtuous depending of the point of view] where as speed increases,liquidity becomes an illusion in the sense that it is good only for trivial amounts of assets.put simply the spread is “retail” and that’s not where you can execute meaningful size.
January 29th, 2007 at 6:33 pm PST
link
jck — yes, exactly. it’s frustrating to read bid-ask studies that very carefully decompose the spread into fine-grained components without supplying a quantity dimension. it’s all noise at 4 share increments. but that doesn’t mean that spread analysis is futile; it just means that quantity has to be considered. one can go deeper into the book, and look at the effective spread for trading 1000 shares (quantity arbitrarily chosen). but, beyond the margin, the book is an ever less complete representation of supply and demand. plus, that approach ignores the good prices available to patient traders, willing to have a go four shares at a time with their ever vigilant algorithms. better to think in terms of pace. if i want to sell 100000 shares, and my time period is 5 days, how much deeper do i have to go beyond the headline “retail spread”. what is the actual spread i have to pay?
btw, very good point that “speed of finance” in and of itself means tighter spreads. non-obvious but self-evident once you’ve thunk it. i never thunk it before. thanks!
January 30th, 2007 at 1:08 am PST
link
This looks very much like some of the things Jack Treynor used to say about the true nature of the spread for informed and uninformed traders.
As far as I can see, though, the engine of your result is that:
a) if hedge funds have an information advantage, they can make money out of it
b) that money comes out of someone else’s pocket.
It is certainly a pretty deep and important point about finance that the spread, and the liquidity of the underlying market, has to compensate for the risk of dealing with someone who has better information than you do. But that’s what’s driving this result rather than anything more complicated.
January 30th, 2007 at 5:14 am PST
link
Daniel,
I have to disagree that the engine of my result (of my conjecture, really) is that hedge-funds ply informational advantages, and other people pay for the price. To the degree hedge-funds are taking advantage of better information about assets and “driving price towards value” (i know, that’s an problematic notion), they ought to be decreasing price uncertainty and diminishing spread. My contention is that they often engage strategies that increase price variability and uncertainty, without requiring unusually good information about anything inherent to the traded assets. The extra costs paid by (long time horizon) market participants go to market-makers, who may or may not be the same hedge-funds, but who must charge more to achieve the same risk-adjusted level of profitability.
I do agree there’s nothing very complicated here. Errr… shorter Steven Waldman:
I do like the pictures, though. I think they are a concise way of emphasizing what is often forgotten, that the liquidity of any asset depends on time and quantity. I think “liquidity surfaces” capture informational aspects of liquidity better than spread analysis or market impact studies. As jck hinted, a market with a tight spread but a steep slope with respect to quantity is not really very liquid, and valuations of the underlying asset are not very certain, despite appearances.
A quibble: The term “adverse selection” is often used in spread analysis to refer to market-maker risk-of-holding, implying as you suggest compensation “for the risk of dealing with someone who has better information than you do”. I think that’s too specific. There is a true “adverse selection” risk that must be compensated, but simple uncertainty in price or valuation must be compensated for as well. No one can know anything at all, but levels of noise can still vary.
January 30th, 2007 at 4:58 pm PST
link
Steve said
I recall an Xmas competition at Wilmott trying to best define Liquidity (in the applied market transactional sense – which is the point of this thread) where winner got Dinner &a Pint at some nouveau pub. And I still find it fascinating to ruminate about, partly because I am in the trenches everyday, and partly because it is the type of rathole into which I enjoy descending.
The first thing that comes to springs to my mind re: your def is that three dimensions do not seem sufficient enough, except for the most gross generalizations. Or, rather, there are all-too-numerous contextual dimensions that ultimately determine the likely liquidity surfaces you contemplate. And like the small quantuum particles whose exstence may or may not be apparent depending upon of host coincidental factors, so to is it for the realized actual liquidity surface versus the numerous (perhaps JLBorgian infinite) potential alternate surfaces, dependent upon the interplay of the contextual status quo. Such context ranges from time of day, weather, the day or month in the year, who’s playing, prior price paths, actions in correlated (and uncorrelated) markets, or in the extreme the number and flutter of butterflies in the himalayas.
The other thing that is missing from the three dimensional model – even with the addition and acceptance of nearly infinite potential and different surfaces related to multiple contexts, is the reflexivity thing. Some of this is algorithmically solvable when one comprehends the nature of a microstructure robotic agent that one is playing against, but in the wider world of men and events, this is, perhaps too complex to actually model.
SO getting back to whether noise traders or hedge funds increase or decrease costs, I do not think there is an answer, for the answer is itself dependent upon teh current market regime and prevailing behavioural and style paradigms. Consider the following: in Q3 2002, following Enron, Adelphia Worldcom, etc. Alfred Harrison of Alliance bought one dip too many, an event that it is likely, turned Alliance (as the 2nd or 3rd largest US equity market particioant) from being the largest marginal buyer “V-dips” to marginal sellers of the same. From one day to the next, the world was turned upside down, especially for other v-dip buyers. No longer could they rely upon someone else’s bid alongside theirs. Markets didn’t clear upon a torpedo and distribution functions elongated. Any look at the higher moments of the cross-section of returns reveals something more bizarre than anything seen in 1929, 1987 1998 or 2000. Each day created a new liquidity surface based upon the context, the surface itself evolving and gyrating reflexively, minute-by-minute, in a feedback-loop gone awry as participants realized that rather than demand increasing with -neg change in price, the more you pushed, the more supply seemed to emerge!
February 16th, 2007 at 2:10 pm PST
link