A toy model of money, growth, and inequality
I’ve been trying to develop my intuitions about how inequality might affect aggregate growth. It’s not like this is a new question. Theoretical arguments have been made both ways, and an empirical literature found a consensus in the 1990s (inequality looked bad for growth), then squinted harder to find little relationship in the 2000s. For some careful theorizing about how inequality might harm growth, take a look at this paper by Philippe Aghion, Eve Caroli, and Cecelia Garcia-Penalosa (“ACG”). They tell three stories, with very careful models: i) when capital markets are imperfect, inequality might reduce the efficiency of investment, as the less productive opportunities of the wealthy are funded in preference to the more productive opportunities of the poor; ii) the borrowing required to fund investment under inequality impose agency costs, because entrepreneurs expend less effort when the benefits and costs of their labors are shared with financiers; and iii) unequal access to investment opportunities may combine with financial market imperfections to create macroeconomic downcycles during which savings cannot be efficiently invested.
Those are good stories, and there are others. The oldest story has to do with incentives. The traditional notion of a trade-off between efficiency and equity comes from the idea that redistribution blunts incentives to invest and produce. In almost any model, reducing after-tax returns on investment will reduce investment, ceteris paribus. It is worth pointing out that inequality and redistribution are separate questions. Inequality may be harmful (or helpful) to growth regardless of whether redistribution by the state would would be good policy. That lower after-tax investment returns reduce growth doesn’t really tell us all that much about the effect of inequality. Also, incentives swing both ways: see ACG story (ii) above, or models of effort in tournaments (e.g. Freeman & Gelber via Benign Brodowicz and commenter Indy).
Anyway, there are lots of stories. I want to add one more, and illustrate it with a very simple model. My intuition goes like this: when people are relatively poor, they spend nearly all their income on real goods and services with care, in ways that yield positive returns in present and future consumption. As people grow wealthy, they spend an increasing fraction of their wealth on financial assets, purchases of which only imperfectly translate to productive mobilization of real goods and services. To make my life as a modeler easier, I conjecture that financial assets are phenomenally inefficient — not only do they fail to yield any positive return, but the net expenditure of real goods and services for financial assets is “thrown into the sea”. We’ll see that despite this, under not-entirely-outrageous assumptions, it might be optimal for wealthy agents to purchase an ever larger “stock” of financial assets, but that by doing so rather than mobilizing real resources, they exert a drag on aggregate growth. We’ll find that transfers (or zero-interest loans) of real resources from the issuers of financial assets to the relatively poor can restore growth, and be Pareto optimal if no deductions are made from the claims of the wealthy when real resources are transfered to the poor. In other words, printing money and giving it to poor people (who then buy real resources from the rich, who prefer the insurance value of money to the use value of their marginal goods) can be optimal and noninflationary. We’ll also find that if there is a monopoly issuer of conventionally “safe” financial assets, the value of those assets can be kept stable even if the issuer totally wastes the real resources it receives in exchange for them, and even if the waste and “insolvency” of the issuer is widely known. Effectively, an arbitrarily insolvent Ponzi scheme can be sustained indefinitely due to the usefulness of having a conventional financial claim that agents can use to pool idiosyncratic risks which they cannot contract to diversify. However, if the economy suffers a shock deep enough not only to halt but to reverse the steady state net positive flow of real goods and services from the economy, a devaluation (inflation) or collapse might occur.
This is a shitty little model, not anything an economist would take seriously. Like most models, it’s tendentious — I set out to confirm my intuition that inequality dampens growth via a financial channel, and I’ve done so. Nevertheless, this what I’ve been thinking about lately, and it’s led me to some unexpected conjectures about money. Please read it, if you must read it at all, as a sketchy first draft. (i know, i am such a girl i’ll never change the world.)
Here’s the setup. There’s a population of rational, risk-averse, agents. At any point in time, each agent can exchange goods and services with other agents, or surrender some of their stuff to a monetary authority (government/banking system) to build a stock of money. (When agents trade amongst themselves, it doesn’t matter whether they use money as a medium of exchange, any money holdings are transient.) The exchange and use of real stuff yields a positive instantaneous return on average, but is risky: sometimes real activity works out, but sometimes it fails. The exchange rate between money and real goods and services — the price level — is notionally fixed. We’ll return to the question of whether this presumption of price stability is credible (without state coercion), since monetary claims will be backed by nothing. We simply assume that, as our story begins, agents believe the price level to be stable. Therefore, they view money as a risk-free asset (that pays no interest; the risk-free rate in our economy is zero). Money is the only financial asset: agents can’t buy or sell claims on one another’s production. So agents cannot diversify their exposure to the risk of their real projects. They must decide at each point in time how much of their wealth to plow into risky real stuff, and how much to allocate to safe money. By assumption, there is no systematic risk: individual project returns are uncorrelated. Agents seek to maximize return while managing undiversifiable idiosyncratic risk.
Some technical points (you can skip this paragraph!): Because it makes the math easy, I’ll model returns as normal, and individual agents as having “constant absolute risk aversion (CARA / negative exponential) utility”. I don’t think the assumption of normal returns hurts us much. (This isn’t like a pricing model where fat tails can kill us — fatter tails would just make our agents look more risk-averse and hold more money.) The CARA assumption is less defensible for the very reason it makes the math easy: Under CARA utility, an agent choosing between a high-return risky and low-return risk-free asset always wants to hold a fixed quantity of the risky asset. That’s unrealistic — even at high levels of wealth, I think people typically expand their holdings of risky assets in absolute terms as they grow richer, although they diminish risky holdings as a proportion of their overall portfolio. That is, it’d be more realistic to use a DARA/IRRA utility function, but with the ones I’ve tried, the math is too hard. Qualitatively, though, this doesn’t matter very much. If agents increase their risky holdings in fixed proportion with their wealth or faster (CRRA or DRRA preferences) my story on inequality breaks down (or reverses under DRRA). But as long as agents put an ever greater fraction of their wealth into money-like assets as they grow rich (and I think they do, for informational as well as risk-management reasons), the basic results holds. The curves below with “kinks” would be smoother under a more realistic DARA/IRRA utility function, but the qualitative implications would not change.
Without further ado, here are some pictures.
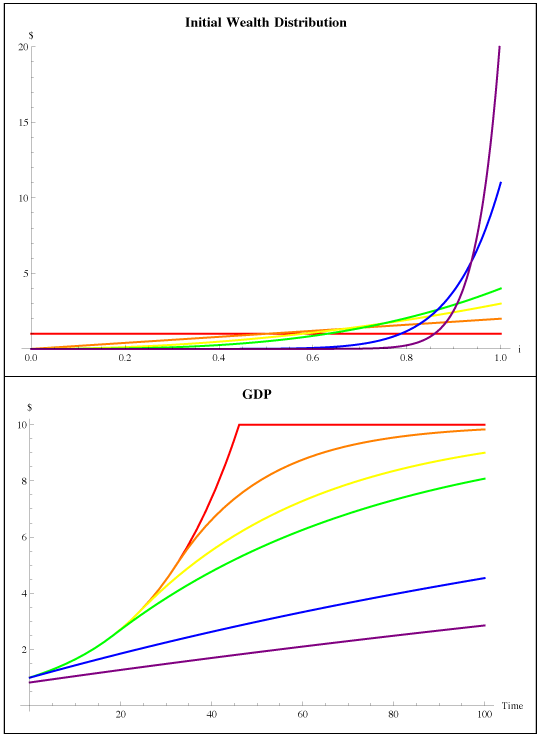
The top graph displays several initial wealth distributions. Imagine a large population of individuals lined up from poorest to richest, with wealth rising from left to right. The flat, red line represents perfect equality. The purple line represents a highly unequal distribution. The bottom graph displays the expected evolution of GDP for each of those distributions. (Curves are matched to income distributions by color throughout.) Eventually the economy reaches a steady state, in this case at GDP of 10 (an arbitrary quantity). But the more equal distributions reach the steady state more quickly than the unequal distributions, because wealthier people exchange part of their wealth for money rather than putting it to productive use in the real economy.
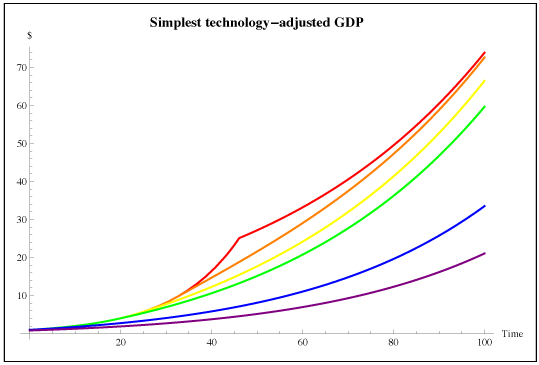
It might seem odd and unrealistic to imagine an economy that just “tops out” and stops growing. This happens because I haven’t modeled technological change. We can easily augment the model with exogenous growth in technology. The easiest way to do that would be to let both investment returns and absolute risk tolerance grow with technology (that is, to let the numeraire be technology adjusted), and set the risk-free rate to the rate of technology growth. Then we get the more comforting graphs below. We could make other choices about how to model technology, “endogenize” it or rethink how technology affects agent preferences, but that’s not what we’re after right now.
Let’s return to the simple, constant-technology model, and see what happens to money. In the graph below, the solid line represents the aggregate perceived wealth of agents in the economy. The dashed line represents real income, GDP, the goods and services that the economy is actually producing. The gap between the solid and dashed line is the stock of money, backed by nothing but nevertheless part of the perceived wealth of agents in the economy.
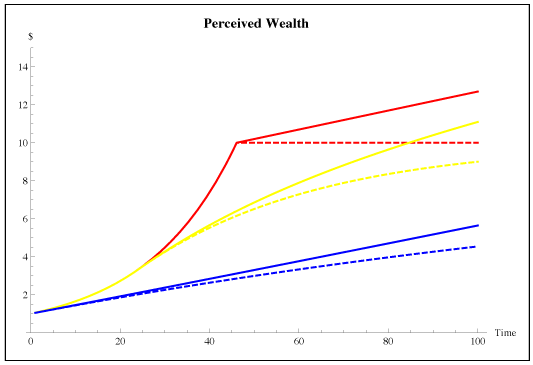
Note that the money stock grows earlier in less equal economies. This is the “leakage” that slows their growth. But for all economies, money growth is unbounded, while (technology-adjusted) GDP approaches a steady state. That is, for all economies, eventually the stock of money gets to be much, much larger than the capacity of the economy to produce goods and services. Is it rational, then, for agents to keep adding to their money stock? Can this be a stable arrangement?
The surprising answer is yes, as long as there is no other risk-free asset in the economy. By assumption, agents who choose not to hold money bear idiosyncratic risk: the value of their holdings, while expected to increase, fluctuates in a manner that they dislike. As long as all agents treat money — backed by nothing at all — as a risk-free asset, and there are many agents whose risks are uncorrelated, each agent knows with almost-certainty that whenever their real projects fail, others will have succeeded more than enough so that the flow of goods and services to the monetary authority will be more more than sufficient to accommodate their idiosyncratic withdrawals. As long as the net flow into money is positive at all times, the aggregate stock money is irrelevant. Each agent values her own stock of money, and wants more, because the greater her stock, the greater her entitlement to make withdrawals should she encounter a string of bad events. The growing illusion of wealth produces real benefits, by leaving agents less insecure than they otherwise would have been. The economy is effectively a Ponzi scheme that, under our assumptions, never fails. More formally, it is a Nash equilibrium: each agent’s best strategy, under the assumption that other agents treat money as a stable risk-free asset, is to treat money as a stable risk-free asset. This is true even when all agents are fully aware of the Ponzi-ish nature of the arrangement.
Of course, this benign result depends upon several assumptions, some of them not so realistic. We’ve assumed that all real investments are uncorrelated and money is the only financial asset. If real investment returns are correlated — if there is systematic risk — it is possible there would be a period during which there would be more losses than gains on real investments. Then, rather than happily exchanging goods and services for money, agents in aggregate would try to redeem money for stuff that financial asset issuers don’t actually have. What then? Our model can’t help us — its assumptions are violated at this point, money is no longer a risk-free asset. The value of financial assets could simply collapse à la Bernie Madoff. But qualitatively, if agents can be made to believe that money will continue to offer some insurance value (and if the expected return on unplanned real investment is low and/or the risks are high), then real goods and services could become more expensive in terms of money until the net flow into financial assets matched the net flow out. Rather than a collapse, there would be an inflation. Here the stock of money matters: under almost any circumstance, dollars offer diminishing marginal insurance value. If there is a large stock of dollar claims, then the devaluation required to match inflows and outflows would have to be larger, as people would surrender dollars more easily. Fundamentally, the degree of devaluation would depend upon the demand curve for real goods in suddenly uncertain dollars. If confidence is shaken just a bit, or people hold few dollars, then demand might be price elastic, and a small revaluation might lead to zero net redemptions. If confidence is shaken a lot, if people hold large stocks of dollars, if some shock creates inelastic demand for real goods ad services, then the devaluation (inflation) could be large. In ordinary times, the stock of money is mostly irrelevant, and in fact large stocks of unbacked money creates real benefits. But in extraordinary times, when the flow into money fails, the stock of outstanding money contributes to the likelihood that an inflation will be violent. (Unmodeled demographic changes, rather than investment losses, could also lead to net outflows and valuation crises.)
If a monetary authority has taxing power, could it overcome a shortfall of inflows of real goods and services relative to desired redemptions by taxing? Under our framework, that’d be a tricky thing to try to do. Taxing the money balances of the wealthy doesn’t much affect the flow of resources, except for agents who would have sufficient balances to cover idiosyncratic losses other than for the taxation. So taxing the very rich does nothing, except alter notional insurance balances, while taxing those with little savings does reduce some flows out of money by forcing people to bear losses as hits to consumption rather than drawdowns of money balances. The most effective form of taxation, however, would be to force the poor to exchange goods and services for money, and then surrender the money to the state. Tax receipts from the poor are all real — they cannot be satisfied by drawdowns of notional money balances, and they reduce the net imbalance between flows into money and redemptions very directly. In other words, taxes are effective at preventing a monetary crisis only to the degree the are regressive and harmful to growth. Taxes on rich people with large money balances are only effective if they are confiscatory, bringing those money balances to near zero.
What if we reimpose our “no systematic risk” assumption, so we don’t have to worry about shortfalls, but allow there to be more than one notionally risk-free asset? Then our Nash equilibrium becomes potentially unstable. So long as agents expect some net positive flow to all monetary assets, they are indifferent among them. But that indifference means that no barrier prevents agents from withdrawing claims from one monetary asset and exchanging it for another. If agent behavior is not random, if trends or “sunspots” might affect financial asset choices, and each agent would try to choose whatever asset they expect other agents would predominantly choose. There could be inexplicable runs to and from assets, similar to banks runs, except under our assumptions all agents already know that all monies are in some sense equally insolvent. Runs might be random (or based on unmodeled markers of “confidence”), unless and until only one survived.
Now let’s consider alternatives to the assumption that real goods and services exchanged for money are “thrown into the sea”. We won’t relax the deep (and important) assumption that aggregate wealth is not storable: it must continually reproduce itself via investment. So the monetary authority doesn’t have the option of simply holding the “stock” of goods and services it collects to back the stock of money. So what if, instead of throwing the stuff into the sea, the monetary authority just gives it away? Let’s consider two cases. First, suppose the monetary authority disburses the goods and services it receives to “poor” people. Under our assumptions that would be a Pareto improvement over ocean disposal. Aggregate growth is maximized, as in the perfect equality case (as all real resources would be continually reinvested until all agents reach their desired risky asset portfolio). Suppose the monetary authority transfers the real goods and services it receives back to the wealthy people who surrendered them? Under our assumptions, this sets up an endless loop. Wealthy people would rather have money than real goods and services, so they’d just sell the subsidy back for money. (Despite the apparent absurdity of this, wealthy people would prefer to receive transfers than have them go to the poor, as they gain insurance value from the notional money stock they build by continually receiving and selling back goods.) Transfers to wealthy people yield potentially unbounded growth in the stock of (still unbacked) financial assets, while transfers to those poor enough to invest in the real economy yield growth. Once the economy reaches its steady state, there are no growth-enhancing transfer possibilities left; all agents can maintain their desired level of real investment without transfers, and transfers just increase the notional money stock. Assuming that the monetary authority can’t invest on its own account, it has little to do with the stuff it receives other than to throw it into the sea.
Instead of making transfers, the monetary authority could lend the goods and services it receives from the rich to the poor. Under my assumptions, those sufficiently the poor would borrow and profitably invest if the interest rate charged is less than the expected return, and if resources are lent at the risk-free rate of zero, all those who hadn’t saturated their risky portfolio would be willing to borrow, and the growth rate could be maximized. This corresponds to people’s intuition about how a perfect or transparent financial system would behave. (Interestingly, if the monetary authority lends rather than transfers, growth might last a bit longer than in the perfect equality or transfers-to-the-poor cases, as agents would have to generate somewhat more than their own desired wealth, because some real wealth would continually belong to the monetary authority during the growth phase. Once the economy reaches the steady state, if the monetary authority cannot invest on its own account, the real wealth it holds is surplus and can no longer be reproduced, and so must be thrown into the sea.
If we imagine that the monetary authority can and does invest on its own account as well as private agents, then inequality doesn’t matter and the economy grows indefinitely at the rate of expected return on investment. If we imagine that the monetary authority can and does invest on its own account, and earns higher returns than economic agents, then inequality would be positive for aggregate growth. If we imagine that the monetary authority does things that yield no return but enhance private returns on investment (for example, creating public goods with the resources it purchases by issuing money), we can’t make any prediction about the effect of inequality without modeling the details.
Some observations: The true heart of this model is the idea that, beyond a certain level of wealth, people prefer the security of saving to expanding personal consumption. In real life, I think this is true of most, but not all, people. It’s a condition that I used to characterize, back in the optimistic 1990s, as “post-affluence” or “post-materialism”. In the steady state of this model, there is wealth inequality but consumption equality. The formerly rich are somewhat better insured than the formerly poor, and savvy investment choices can further increase agents’ degree of security (or position in status competitions), but people are satisfied with their level of consumption and don’t much alter it. Changes in consumption patterns result from changes in technology rather than idiosyncratic improvements in economic circumstance. I think this is a state of affairs worth thinking about. Again, in reality, people are not identical, both in terms of levels of consumption at which they’d be content and propensity to switch from consumption to savings at high levels of wealth. But in the 1990s, in my little bubble of opportunity-rich tech types, I did wonder whether we might become a “post-affluent” society, something like what the steady state of this model suggests.
One interesting characteristic of this model is that poor immigrants are good for aggregate growth. As the economy grows, agents become rich and content and cease contributing to growth. Importing poor people who are still striving creates growth and increases steady state GDP, but not GDP per capita (although one could posit indirect spillovers from aggregate growth to technological change, public goods provision, or somesuch). I think there’s something to that.
Some semi-technical miscellany
For simplicity, we’ve assumed (unrealistically) that all agents have identical preferences and opportunities. They only differ in their level of wealth. In the real world, peoples’ opportunities and risks vary. In the real world, there are a wide variety of financial assets, some financial asset purchases do affect real investment, and people choose to purchase financial assets rather than real assets in order to capture return, not just to hedge the risks of their own real lives. People may choose financial assets over real assets due to informational problems: high return projects may be available, but it may be difficult or costly to discover them. This model assumes all that away. Agents always know the return distribution they face for real investment; both risk and return are constant. In reality you’d expect diminishing marginal returns to risk (for any given search cost). These effects work in different directions: the fact that financial investment does affect growth-producing real investment by business and government means we are likely to overstate the cost of inequality in the model, but the model excludes many reasons for purchasing financial assets, so it potentially underestimates the scale of inefficient financial asset purchases.
We haven’t drawn a distinction between wealth and income inequality, because under the assumptions of our model, real income is always proportional to real wealth. However, perceived wealth includes monetary holdings. Under our assumptions, income eventually decreases as a proportion of perceived wealth, as agents invest in nonyielding money. In the steady state, there is perfect income equality, although the rank order of perceived wealth is preserved (in expectation) from the starting distribution.
We haven’t drawn a distinction between “consumption” and “investment”. If agents are rational and have time-consistent preferences, the distinction is immaterial: agents make purchasing decisions that yield a stream of consumption over time, and there’s no reason to treat the enabling of consumption at time zero any differently from consumption at time seven as long as the allocation is optimal. We concern ourselves only with “real expenditure”, and the returns thereon. Our intuitions about the distinction between consumption and investment have to do with lived knowledge that people’s preferences are not time-consistent, that it is hard to defer consumption however “rational” that might be. But even intuitively the distinction between consumption and investment is murky. Is eating consumption or investment? On the one hand, to eat is literally to consume. On the other hand, failing to eat reliably leads to reduced future returns on labor. Maybe some minimal “necessary eating” is investment, and the rest consumption? But we have a notion of poor investment for other goods. Why is it better to consider eating dessert “consumption” rather than superfluous and foolish investment?
I’ve been very vague throughout about the distinction between “financial assets” and “money”. That’s intentional but sloppy. Money is the purest example of a financial asset arguably backed by nothing, whose issuers (both governments and banks) may waste, lend, or transfer the real goods and services they receive in exchange for the funds they issue. But other financial assets may be similar, if people purchase them because they seem safer than forward-looking personal spending, and if net issuance results in transfers, loans, or manager perqs rather than direct productive investment. Financial assets whose issuance funds the purchase of real capital goods would count as risky investment rather than money in our model. I also need to think about how purchasing appreciated assets in secondary markets fits in: I think there should be something of an equivalence between assets like money whose increase in aggregate value takes the form of new issue under nominal price stability, and less supply-elastic financial assets which see price appreciation rather than new issue.

“and an empirical literature found a consensus in the 1990s (inequality looked bad for growth), then squinted harder to find little relationship in the 2000s.”
Very blunt statistical work, with little data and controls, and super unrealistic assumptions, with a ridiculously oversimplified data generating process, all literally interpreted, will often not tell you much and/or mislead.
You really need to be smart here in the statistical work you do and how you interpret it. And you have to rely on the far more data than the standard formal statistical data. It may just have very little power when you ignore the vast amount of other data.
Clearly you can make a very compelling logical argument linked back to very realistic assumptions (especially compared to the typical standards of large scale statistical work in economics) that not investing in the bulk of your people because they aren’t rich will mean foregoing a tremendous amount of national economic growth and wealth.
January 23rd, 2010 at 8:32 pm PST
link
Elaborating — It really depends on how much inequality, and what anti-inequality programs are implemented.
Implementing pure equality, like via extreme communism, is horrible for growth and wealth creation.
But going from a laissez faire economy, where you’re completely on your own, to one where you at least provide free public schooling for everyone, would mean a tremendous increase in national growth and wealth.
A smart schoolfare program would be great for growth and long term wealth creation. A program of just giving large sums of money forever to anyone, even able bodied, for not working, would be very bad.
Your statistical work has to differentiate between different kinds of anti-inequality programs and different degrees. In other words, you have to be very smart here. You have to use high level thinking, not mechanical, literal interpretation to reality thinking.
January 23rd, 2010 at 8:43 pm PST
link
The inequality-growth curve can be inverted U shaped. Curves don’t always have to be monotonically increasing or decreasing. Many times they, in reality, have much more complicated shapes.
January 23rd, 2010 at 8:50 pm PST
link
> when people are relatively poor, they spend nearly all their income on real goods and services with care, in ways that yield positive returns in present and future consumption. As people grow wealthy, they spend an increasing fraction of their wealth on financial assets, purchases of which only imperfectly translate to productive mobilization of real goods and services.
this doesn’t fit my understanding. why are saving rates so much higher as a percentage of income in china than they are here?
January 24th, 2010 at 12:35 am PST
link
babar — so the claim would be within a culture (really within an individual), not cross-culturally, the household savings rate in China vs the US doesn’t tell us very much. the question would be, as people get wealthier in China, do they tend to save more or less is money-like financial assets (i.e. assets the purchase of which is pretty much uncoupled to real investment decisions).
my casual (and perhaps inaccurate) understanding of Chinese savings behavior is that even poor households save a lot as a substitute for social insurance that is state-provided elsewhere. insurance, in my story, is the fundamental motivation for holding money, but one might argue that access to emergency medical care and avoidance of really abject poverty in a crisis or during retirement is so valuable that very poor people prefer to build social insurance balances than to invest in consumption growth. But then once a social insurance balance is established, agents would strive to increase consumption, until they become wealthy, after which marginal income is again saved as money or financial assets. if so, “middle class” income would be growth-enhancing, relative to income of both the very rich and the very poor. In societies with good social insurance, no one is that poor (as everyone holds valuable financial assets as a matter of right), so the low end of the income distribution behaves like the middle class in countries with weak social insurance.
fundamentally this is an empirical question, and it’s muddied by the fact that richer people hold substantial wealth in risky financial assets, whose quantity or prices may affect real investment. if wealthier people buy stock, does that spur real growth as well as direct purchases of durable goods or productive services?
one important note whenever China’s very high savings rate comes up: while Chinese households do save a lot relative to the US or Western countries, most of China’s aggregate savings comes from retained earnings by businesses (often state-owned enterprises) held in money balances. (that would not in my model be very growth enhancing, and i’ll claim that China’s growth depends on imported consumption offsetting the consumption the state suppresses domestically.) if i recall, China’s household savings rate is comparable to India’s, consistent with the social insurance story.
January 24th, 2010 at 3:33 am PST
link
[…] A toy model of money, growth, and inequality Steve Waldman […]
January 24th, 2010 at 4:05 am PST
link
richard — i’m with you on statistical work, both in general and in the specific case. given the necessity to choose an empirical model and the huge space of potential models (and the likely complexity of reasonable models), the value of empirical work is always a matter if judgment. i don’t think the growth regressions of the 1990s that showed a negative relationship between inequality and growth, or the newer revisionist literature that changes the models and finds little effect, tell us very much at all.
it’s certainly true that the effect of inequality on growth could switch directions. in fact, the “traditional” view on the subject is the kuznets curve, under which “middle income” countries are expected to be unequal, but very rich or poor countries less so. One could pick-up on babar’s point re the demand for financial savings at low income in countries with poor social insurance to suggest that poor countries grow by becoming more unequal (only the rich are willing to undertake real investment as the poor save in lieu of social insurance) while middle income countries benefit by becoming more equal (the very wealthy hold build financial asset stocks while the middle class undertake real projects).
i agree with many of your broader points, although i do think we should explore using transfers more (or money-funded disbursements). i think the adverse incentive effects and the inflationary effects of giving very modest incomes to everyone as a matter of right may be overstated (though i’ll admit i could be wrong, and it’s a potentially risky sort of idea).
January 24th, 2010 at 5:13 am PST
link
[…] Taxes are effective at preventing a monetary crisis only to the degree the are regressive and harmful to growth. Taxes on rich people with large money balances are only effective if they are confiscatory.Close […]
January 24th, 2010 at 5:44 am PST
link
[…] interfluidity » A toy model of money, growth, and inequality Share and […]
January 24th, 2010 at 6:38 am PST
link
>i agree with many of your [Richard Serlin’s] broader points, although i do think we should explore using transfers more (or money-funded disbursements). i think the adverse incentive effects and the inflationary effects of giving very modest incomes to everyone as a matter of right may be overstated (though i’ll admit i could be wrong, and it’s a potentially risky sort of idea).
While my intuition also tends to suggest flat transfers to every citizen as the most efficient mechanism for growth in a high-productivity economy, at the very least we should take to heart Lane Kenworthy’s work and greatly expand the Earned Income Tax Credit. (See in particular the last chapter of Egalitarian Capitalism.)
This proposal has the dual benefits of being economically efficient, and (more) politically palatable within a puritanical culture.
Steve
http://asymptosis.com
January 24th, 2010 at 9:08 am PST
link
[…] A model that helps explain how inequality might effect economic growth. (Interfluidity) […]
January 24th, 2010 at 9:32 am PST
link
You need to retool your entire method of thinking.
At any given moment there is a fixed supply of capital, land, labor. Labor changes slowly over the long-term, land does not change at all, and capital changes dramatically. Within any economy, these resources are devoted to various productive needs. In a boom, close to 100% of capital may be allocated. In a recession, somewhat less than that. When money is redistributed, that simply means the right to allocate these resources has been redistributed. If wealthy get richer, they have a greater claim to these resources than before. If the poor get richer, they have a greater claim to these resources than before. If they give the money to a banker to invest, the banker has a greater claim to these resources (temporarily). How would the investor redistribute resources? Based on assigning land, labor, and capital for the greatest expected returns, which are in turn based on predictions of how people will exercise there right to redistribute resources.
Under this way of thinking, resources are not lost. There may be slower growth if resources are focused more on present day needs, and less on the future. And if they are invested inefficiently due to poor predictive ability of future desires. But you have to remember goods are not money, so they cannot be thrown away in the same sense.
Now, if we think like this, what impact will a change in wealth distribution have on the economy? It will change how goods are allocated. For example, wealthy people tend to have a higher savings rate, so there would be an increase in the ammount of resources allocated toward producing capital producing goods rather than in producing consumable goods.
I leave the rest of the conclusions to you.
—–
PS
Your model has so many unrealistic assumptions that it is irrelevant. You can only make simplifying assumptions (like the earth is the size of an infinitely small dot, when dealing with gravity) if they make it so you are virtually correct.
January 24th, 2010 at 11:31 am PST
link
Steve,
Be aware that mathematical modeling is a disease promoted by attending graduate school.
It can result in a condition in which the model is preferred to signals originating in reality, e.g., Ben Bernanke’s behavior after the failure of WaMu that wiped out the creditors without significantly disrupting banking on the West Coast or anywhere else at all.
Be careful!
Regards,
Benign
January 24th, 2010 at 3:24 pm PST
link
SRW,
I think your “sketchy first draft” of a “shitty little model” is in part a stealth application of Chartalism, with an income/wealth distribution twist. But I found it challenging to reconcile, when you started talking about “redemptions” and “withdrawals”.
“At any point in time, each agent can exchange goods and services with other agents, or surrender some of their stuff to a monetary authority (government/banking system) to build a stock of money. (When agents trade amongst themselves, it doesn’t matter whether they use money as a medium of exchange, any money holdings are transient.)”
This confirms the transfer of real output from the private sector to the public sector in exchange for money. The public sector supplies “net financial assets” to the private sector in the form of money. Chartalism refers to the NFA interface as the exogenous or vertical part of the system – the fiat component. (The real world interpretation includes bank reserves, currency, and bonds. Your model only specifies money, which can be interpreted as a deposit by anybody with the monetary authority.) The second sentence is consistent with what Chartalists refer to as the endogenous or horizontal component of the system.
The gap in your wealth to GDP charts is in effect the net financial asset concept of Chartalism. It is the supply of net saving created by the government for the private sector. It is created through the purchase of goods and services in exchange for money in this case. It also represents a budget deficit.
“As people grow wealthy, they spend an increasing fraction of their wealth on financial assets, purchases of which only imperfectly translate to productive mobilization of real goods and services.”
My own intuition is that as people get rich, they save more of their income. Their consumption approaches an upper bound relatively quickly. When people remain poor, they consume more of their income, but fall short of their potential upper bound. They may force themselves to do a bit of saving, but they remain well below their consumption upper bound. The rich approach their upper bound asymptotically; the poor don’t.
With a redistribution of income from rich to poor, the poor will quickly increase their consumption because they are well below their upper bound. Conversely, the rich have been parked near their consumption upper bound for some time, and have excess saving to work through before feeling poor enough to start decreasing their consumption at any decent pace. The net result is that with redistribution, aggregate consumption/ investment increases; GDP and aggregate wealth increase.
“Is it rational, then, for agents to keep adding to their money stock? Can this be a stable arrangement? The surprising answer is yes, as long as there is no other risk-free asset in the economy.”
This is pure Chartalism. The government is the only supplier of “net financial assets” to the endogenous private sector system. That’s equivalent to the idea of “no other risk-free asset”.
“The flow of goods and services to the monetary authority will be more than sufficient to accommodate their idiosyncratic withdrawals.”
Here, I’m confused by your use of “withdrawal”. It is possible that I’m completely misinterpreting your meaning in this case, as well as in your use of “redemption”. But here’s my take:
Government created money cannot be “withdrawn” in aggregate if that is what you are referring to, apart from taxation. Taxation effectively destroys government issued money by the amount of the tax (Chartalism again, but reflecting real world accounting). Withdrawal in this aggregate context can only refer to money destruction via taxation. But don’t think that’s what you meant.
If instead you are referring to the use of money circulating from one user (withdrawer) to the next (depositor), that’s OK. In that context, the dynamic again is pure Chartalism. The non government sector provides goods and services, which the government purchases by creating money (and deficits). “Idiosyncratic withdrawals” is then equivalent to the Chartalist idea of demand for net financial assets, in the sense that the supply of net financial assets facilitates the use of the money that has been created in transactions and in sequential withdrawals and deposits using the same supply of money.
“Each agent values her own stock of money, and wants more, because the greater her stock, the greater her entitlement to make withdrawals should she encounter a string of bad events.”
Again, this is the non government demand for net saving, which is particularly strong in a recession. And withdrawal only makes sense in the context of an individual depositor withdrawing for use in a transaction with some counterparty who then deposits the same amount back with the money issuer.
“The gap between the solid and dashed line is the stock of money, backed by nothing but nevertheless part of the perceived wealth of agents in the economy.”
This gap is the “net financial asset” position in the Chartalist decomposition of government and non government sectors.
“The economy is effectively a Ponzi scheme that, under our assumptions, never fails.”
Chartalists would object to Ponzi, of course. But a fiat currency issuer can never fail technically. And net issuance proceeds provided that there is still residual private sector demand for net financial assets, prior to inflationary pressures becoming a threat.
“If a monetary authority has taxing power, could it overcome a shortfall of inflows of real goods and services relative to desired redemptions by taxing?”
Here you use the word “redemption”. This is the sentence in the post that leaves me most bewildered as to the intended meaning. If there is a “shortfall” of real inflows, then there is a shortfall in goods and services sold to the public sector in exchange for money. But I can’t figure out what the relevance or meaning is of “shortfall” as a comparative. So real sold are down. Money issued is down. But I don’t know what this has to do with “redemptions” or taxation.
Notwithstanding that, there is a strong connection between redemptions and taxation, quite independent of “shortfalls”. Taxation is the only means of “redeeming” government created money, when money is the only financial asset. Taxpayers present the store of value as the means of payment, according to the specified tax liability, thereby redeeming it as a financial asset. Net saving in the form of money is destroyed. But I can’t relate “shortfall” to either redemptions or taxation.
“The most effective form of taxation, however, would be to force the poor to exchange goods and services for money, and then surrender the money to the state. Tax receipts from the poor are all real — they cannot be satisfied by drawdowns of notional money balances, and they reduce the net imbalance between flows into money and redemptions very directly.”
Well, that is how taxation works in fact, for the rich and the poor. But again I don’t understand your meaning in terms of a balance of flows into money and redemption of money. That redemption just doesn’t happen, unless indeed it is through taxation.
“Money is the purest example of a financial asset arguably backed by nothing, whose issuers (both governments and banks) may waste, lend, or transfer the real goods and services they receive in exchange for the funds they issue…each agent knows with almost-certainty that whenever their real projects fail, others will have succeeded more than enough so that the flow of goods and services to the monetary authority will be more more than sufficient to accommodate their idiosyncratic withdrawals. As long as the net flow into money is positive at all times, the aggregate stock money is irrelevant. Each agent values her own stock of money, and wants more, because the greater her stock, the greater her entitlement to make withdrawals should she encounter a string of bad events.”
Again, I’m trying to figure out what “withdrawals” you’re talking about here? It can’t be aggregate money, as I’ve described. And it doesn’t make sense for it to be aggregate real goods. Agents don’t make withdrawals after real goods and services are moved from the private sector to the public sector. E.g. the public sector pays for a bridge built by the private sector by creating money. The private sector doesn’t buy that bridge back. The private sector earns income equal to the money paid, and saves that income as “net financial assets” – in this case, in the form of money. The bridge is not then “withdrawn” in exchange for the redemption of money. The public sector itself doesn’t generate real goods and services so it can’t sell them to the private sector.
Each agent values her own stock of money, and wants more, because the greater her stock, the greater her entitlement to make withdrawals should she encounter a string of bad events.
There is no withdrawal of the stock of money. There is only use of the existing stock. It circulates. It is not destroyed by “withdrawal”. It is the same thing in the commercial banking system – money is not destroyed or used up simply because it is “withdrawn” from a particular deposit account. It ends up in another.
I’m not sure what is meant by “thrown into the sea”. I suppose it could mean a bridge that is built in exchange for the issuance of new money, where the bridge collapses the next day. Or it could mean a money transfer created by “helicopter drop” that is then used to buy perishable goods and services.
Thanks as always for a thought provoking post.
January 24th, 2010 at 4:08 pm PST
link
“But as long as agents put an ever greater fraction of their wealth into money-like assets as they grow rich (and I think they do, for informational as well as risk-management reasons), the basic results holds.”
This is unfortunately (unfortunately for your model at least) not true. There is an overwhelming evidence that:
1. High income people hold a SMALLER fraction of their wealth in cash and cash-like assets.
2. High income people hold a LARGER fraction of their wealth in long-term, stock-like assets which would qualify as productive according to your reasoning.
See for instance Avery et al (1987), Wolff (1983), Erosa and Ventura (2002), Kessler and Wolff (1991), Kennickell and Starr-McCluear (1996) and many many others.
The fact that the evidence is so strong is exactly the reason why a model like you have developed is not considered in the literature. It is immediately disqualified by the data.
A second comment is technical and regards the fact that valuable money survives in your rational model despite the fact that it plays no role. Unless you are making a simplifing assumption somewhere, or you have a component of the model that you do not spell out, this does not seem to be correct. See the seminal paper by Santos and Woodford on the (im)possibility of bubbles in rational models. It is hard to cook such a model up. Not impossible, but I don’t see in your model how it would work. Is it possible to see the actual model, written down, with the solution?
This does not imply that inequality is unimportant. But I strongly believe that you are taking the wrong approach here. Whenever I think about cases when could inequality have a harmful effect on economic growth, I come to a conclusion that slow growth and high inequality are symptoms of another problem (like insufficient access to education, high cost to cooperation etc.). I believe that if you take inequality as given and you will try to construct a model where inequality directly causes slow growth, you will not find a satisfying answer. Even worse, it moves you away from the true causes.
January 24th, 2010 at 4:24 pm PST
link
Let me put it more simply: It doesn’t (fundamentally) matter who decides where capital should be allocated, so it is impossible to know what the results will be of increasing inequality. All that matters is what percent of capital is allocated toward future production (i.e. new factories), and what the returns on these investments are.
Matt
January 24th, 2010 at 4:34 pm PST
link
SRW:
What’s your assumption on the distribution of the ability of the underlying population? Are people, fundamentally “equal” to start with or are they not? If not, how “unequal” are they?
January 24th, 2010 at 4:40 pm PST
link
I agree on the reference to chartalism, I also see some influence by Hyman Minsky. I’ve been casting about for a modeling that could be used to describe the results of the USDA BAE/Calif. Bureau of Reclamation study by Goldschmidt on Dinuba and Arvin. Dinuba and Arvin could be treated as cases within a domain of possible sets of applications. I don’t believe that anyone has ever applied this sort of process to that research. Yes, modeling is not perfect, and if that is taken as a given then the modeling process can also be useful. Under the category of chartalism various models for monetary reform could be generated. I am going to absorb this as much as I can. This seems to have the capacity for both micro and middle range type simulations.And there seem to be other possibilities. ideasinc@ee.net
January 24th, 2010 at 5:17 pm PST
link
All — Wow. Thanks for a lot of really thoughtful comments.
JKH, Tadit, and of course winterspeak — Chartalist ideas are definitely toying with me these days. I didn’t initially intend this to be a toy Chartalist economy, but that’s what it became, and actually I find that aspect at least as interesting as the inequality issues I set out to address. I’m trying to understand, basically, whether and under what conditions the sort of economy described by Chartalists could be stable and productive. An unintended conequence of this exercise, has been to diminish (though not eliminate) my skepticism of Chartalism as an overt policy framework.
winterspeak — The model assumes that all agents are identical, besides an initial income/wealth distribution. They are exposed independently to random shocks, bot those shocks are drawn from identical distrbutions. I don’t mean here to address questions of what level of inequality might be efficient if agents have different levels of productivity viz their behavior in the real economy, although if I got the model a bit tighter, it might be possible to play with that in this framework and see what happens.
January 24th, 2010 at 6:11 pm PST
link
pinus — if we take “nonproductive financial assets” to be simply cash and government securities, as I do in the formal model for simplicity, then you may well be right. Within peoples’ financial asset portfolio, it is certainly not clear that as people get wealthy they prefer a greater fraction of cash-like assets, and the opposite case may well be stronger.
but my claim is that financial assets in general are more money-like than factory-like. that is, when i purchase a share of IBM in a secondary market, at the margin I may be increasing the likelihood that IBM builds a factory or hires a new programmer, but the relationship is tenuous, and nothing like the one-to-one relationship that would have obtained if I’d hired and supervised a programmer myself with the same money. the real financial sector is very complex and gelatinous. it does not help very much to rely on the primary/secondary market distinction: even if I buy an IPO share or seasoned issue, my funds may be transfers inside stakeholders selling, or the firm may simply hold the capital itself in financial assets. purchases of stock on secondary markets are often not a net-zero exchange but are drawn from exchanges of real goods and services for financial assets: to sketch, I exchange real goods and services for money, then I exchange my money for a share of IBM for $X. The net effect is real goods and services go to the monetary authority, the stock of financial assets increases. The fact that I myself hold IBM shares rather than money is unimportant. Shares of stock and other “risk assets”, then, are more like unproductive money then real investment in the model. Plus, most wealthy investors hold “risk” financial assets for the same reason they hold money, to hedge against idiosyncratic risk and demand for future consumption. In order to make financial holdings more money like, and less like the deliberate mobilization of real assets, they hold diversified portfolios.
I might alternatively supply real goods and services to IBM in exchange for shares which they issue de novo or repurchase in secondary markets. Then I hold a financial asset, have failed to directly mobilize some real goods and services, and the question becomes the efficiency with which IBM makes use of the resources I have supplied. In other words, every issuer of financial assets is in a sense a monetary authority, and to get some sense of the effect of wealth on investment we have to take the aggregate portfolio of financial assets, valued at the cost of the real goods and services for which they were issued, and compare the productivity of those assets to more direct investment. I think if we did now, we’d find that while some issuers of financial assets mobilize real goods and services much more productively than individuals do, as the aggregate financial portfolio grows, the efficiency of mobilization diminishes.
This is an empirical, not a logical claim: if individuals in the model can mobilize resources productively, there is no a priori reason why firms should not be able to do so with resources they receive in exchange for financial claims. But I think that, in fact, for informational reasons and because most projects face diminishing marginal returns beyond a certain scale, wealthy investors are not able to select and discipline financial portfolios as productively as individuals manage their own real investments. The conventional reliance on diversification and the possibility that financial capital flows may induce entry by agents seeking to capture rents rather than efficiently direct capital support my case.
i’d add that there’s probably a “laffer curve” here: obviously there are often economies of scale prior to diseconomies associated with diminishing marginal return, and in real life, people have proven much more productive by organizing in formal enterprises rather than by ad hoc direct activity. if so, rather than a monotonic drag on growth from inequality, we might find, for any given wealth/technology, an optimal portfolio of financial assets. if we take as given both optimal selection and that the rich buy financial assets, then there would be an optimal degree of inequality, prior to which or beyond which growth would be stunted. if we relax those assumptions, then we have to address issues of selection and insurance. if the rich generally purchase diversified portfolios as insurance, and the poor are willing to buy financial assets when they are carefully selected to be at least as productive direct real-economy investments, then inequality remains harmful to growth. if the rich purchase optimally productive portfolios, and the poor are behaviorally averse to financial assets, then inequality would enhance growth.
This is a lot. But basically my response to your critique is that diversified portfolios of “risky financial assets” purchased by the wealthy are more like money than real investment.
January 24th, 2010 at 6:42 pm PST
link
Pinus:
I’m with you.
SW:
I say look to Argentina and Venezuela. When the monetary authority prints too much of his stuff what do people in the real world do? If they can’t buy gold, they look for alternatives. These may include second: refrigrators, radios, washing machines, televisions and cars. Look at China today. The PBOC is going hog wild creating Yuan. I think China’s money stock increased about 30% last year. Chinese people respond by buying second homes. What? Second homes in supposedly Communist China? Yes. I don’t buy this model at all.
Happy New Year.
IA
January 24th, 2010 at 6:57 pm PST
link
I agree with pinus that you’ll not find a satisfying answer to modeling growth directly from inequality. The microeconomic rationale for the model matters. I’d be happier with a model relating growth and inequality to information asymmetries (maybe there’s already one – I’m not an expert.)
I can understand that in a society plagued with few social norms, laws or regulations to prevent “rip-offs,” people might be less inclined to engage in potentially Pareto optimal transactions and growth could be slower than it otherwise might. For the transactions that do occur in such societies, those on the information-rich side could generate much more income and wealth. If I believed that inequality was generated in this fashion, I’d be much more concerned about it than if I didn’t believe I was being misled at every purchase. If information asymmetries “caused” the inequalities and slow growth, then solutions might arguably be directed toward contract law, regulation or improving the social contract rather than monetary or tax policies.
I suspect that even in a utopia where nobody tried to take advantage of others ignorance when making a transaction (the parties tried to ensure that any information asymmetries present would change the nature of the transaction), you’d still have substantial income and wealth inequalities. I’d even conjecture that this distribution of income/wealth might be in some sense ‘optimal’ and that efforts to either reduce or increase variation in income/wealth would lead to lower growth.
As pinus mentioned, there are probably many problems besides information asymmetries which directly contribute to slow growth. Defining and measuring “useful” growth also seems difficult – at least to this non-economist.
Steve – Looks like you’ve worked hard on this. Good try – but I just don’t think I’ll ever be convinced to take actions to reduce (or ignore) inequality by anything like this line of reasoning. Like most people, I could make more money if I wanted to – I just value my leisure time more than the money. Similarly, I don’t begrudge those who make a lot of money because they are willing to take on roles in society that I can’t or won’t take on. I think most are willing to concede that some income inequalities are necessary. Inequality may be a symptom, but almost certainly not the cause of the underlying disease. Treating it without understanding the cause will probably do more harm than good.
January 24th, 2010 at 7:00 pm PST
link
[…] A toy model of money, growth, and inequality – Via Interfluidity – I’ve been trying to develop my intuitions about how inequality might affect aggregate growth. It’s not like this is a new question. Theoretical arguments have been made both ways, and an empirical literature found a consensus in the 1990s (inequality looked bad for growth), then squinted harder to find little relationship in the 2000s. For some careful theorizing about how inequality might harm growth, take a look at this paper by Philippe Aghion, Eve Caroli, and Cecelia Garcia-Penalosa (”ACG”). They tell three stories, with very careful models: i) when capital markets are imperfect, inequality might reduce the efficiency of investment, as the less productive opportunities of the wealthy are funded in preference to the more productive opportunities of the poor; ii) the borrowing required to fund investment under inequality impose agency costs, because entrepreneurs expend less effort when the benefits and costs of their labors are shared with financiers; and iii) unequal access to investment opportunities may combine with financial market imperfections to create macroeconomic downcycles during which savings cannot be efficiently invested. The Age of Affirmation – Via Farnam Street & Miller Mcune – The study in the December issue of Media, War & Conflict by Shawn Powers, a fellow at the USC Center on Public Diplomacy, and Mohammed el-Nawawy, an assistant professor in the department of communication at Queens University of Charlotte, found that the longer viewers had been watching Al Jazeera English, the less dogmatic they were in their opinions and therefore more open to considering alternative and clashing opinions. […]
January 24th, 2010 at 7:02 pm PST
link
“Steve – …I think most are willing to concede that some income inequalities are necessary. Inequality may be a symptom, but almost certainly not the cause of the underlying disease. Treating it without understanding the cause will probably do more harm than good.”
—
If you make a comment like that you have lost all claim to impartiality. You obviously are approaching an economic question with a giant bias.
January 24th, 2010 at 8:12 pm PST
link
JKH — First, thanks for the very extensive, specific, and thoughtful comments (although of course I expect no less of you).
As I’ve already said, your accusations of closet Chartalism are on point, although outside the oversimple formal model, I’m trying to struggle with the heterogeneity of financial assets, while Chartalists (and the formal model) take as given a stable, monopoly money supplier.
First, I want to clear up the confusion about “redemptions” and “withdrawals”, within the context of the simple formal model. This is my bad, as these ideas were evolving in my head as I was writing this sketchy first draft. But I did come to a resolution.
Here’s the deal, within the model. The monetary authority issues financial assets, but does not permit redemptions or withdrawals on net. That is, since real resources, once they are exchanged for money, are “thrown into the sea”, the monetary authority has no means of accepting money and disgorging goods and services.
However, there can be gross redemptions. The monetary authority might choose to intermediate these or not — it doesn’t matter. All that matters is that for any given individual who wishes to “redeem” a dollar, there must be some other individual who wishes to “deposit” real goods and services in exchange for money. For an aura of realism, imagine people exchange goods and services for money amongst themselves, and only deal with the monetary authority when there is a net imbalance, that is when (at the conventional price level, which the monetary authority seeks to maintain) there are either more people who wish to exchange goods for money, or more people who wish to diminish their money balances in exchange for stuff. But the monetary authority is bound by a zero-net-redemptions constraint: If someone walks up to the Federal Reserve Bank in our little terrarium and tries to get a prize their green paper, the gecko called Ben has nothing to offer other than some cool lizard facial expression. So, one of the ramifications of our model is that, as a precondition of stability, the monetary authority must manage things so that the desired flow into money (the desire of agents to exchange goods for money at the conventional price level) is at least as great as the desired outflow (the desire of agents to purchase real goods and services for money). When the zero-net-redemptions constraint is violated, when desired net redemptions are greater than zero (no prob if they are less than zero), devaluation or collapse ensues. BTW, I’m using redemption and withdrawal interchangeably.
One tricky issue is how and when the stock of money matters. Unless a collapse is total, it’s clear that money stocks should matter once the zero-net-redemptions constraint would fail at the conventional price level, because the revaluation that would be required to restore balance would depend upon the demand curve for goods and services in absolute dollars, and that in turn would depend upon money stocks. But do nominal money stocks matter prior to a failure? Under the assumptions of the model, no. But suppose we add idiosyncratic “luxury” withdrawals (by individuals) the expected size of which grow with individuals’ stock of money. That’s a pretty plausible extension, and creates an outflow of money that grows in proportion to absolute balances. In this case, the monetary authority must manage absolute balances in order to manage flows. Suppose also that there are potential alternative monies, that flows to these alternatives are proportional to stocks of conventional money, and that the rate of flow to a monetary authority grows faster than linearly, as flows beget flows. Then, again, the stability of the monetary system requires that the monetary authority manage absolute money balances, and may find itself in a situation where flows to alternatives will foreseeably force a violation of zero-net-redemptions, in which case it might have to use coercive authority (if it can) to restrict flows to alternative monies.
Note that I use “idiosyncratic withdrawals” to mean the occasional and unpredictable desire of some individuals to net-trade money for goods and services, even though in aggregate individuals are building money stocks. “Aggregate withdrawals” are where there comes to be a problem.
In my view, a Ponzi or a monetary system “fails” when it becomes unable to meet investor claims in terms of real promised value. Bernie Madoff investor claims were never worthless: there were always some assets behind his investment fund. But the value of those claims, in terms of real goods and services or US dollars, became far less than what had been promised to investors once Madoff could no longer match inflows to outflows. Similarly, it is not very interesting to me that a fiat currency issuer cannot “fail” in the tautological sense that it can always deliver the claims it has promised. A fiat currency issuer also promises (explicitly or tacitly) to maintain some degree of price stability. That might not be perfect and deterministic, and measuring real-world price levels is largely a theological exercise. But in my view a monetary system fails when holders of money cannot redeem claims for goods and services at prices “reasonably close to” what managers of the monetary system have permitted them to expect. Degrees of loss matter, and one thing I don’t think we understand very well is what determines how “badly” a monetary system fails when it fails. Even the word “fail” is too binary: if US inflation were to jump to 3%, would that constitute “failure”? We’re really interested in the dynamics of monetary systems and Ponzi schemes, with less attention to the labels. Why is it that even a modest deficiency of inflows relative to outflows kills a Madoff but not a US Dollar? I think that has to do with things like brittleness of expectations and the availability of alternatives more than any fundamental distinction. And of course, as the Chartalists I think overemphasize, a monetary authority is a Ponzi scheme with the power to tax, to force inflows (that are then confiscated) to help sustain balance.
Re taxes, you write…
“Shortfall” is always comparative. It refers to gross quantity of money demanded for goods relative to gross quantity of goods for money demanded at conventional prices. The job of a monetary-system/Ponzi-scheme/business-firm manager is to ensure that now and at every future time there will be sufficient inflows of resources (exchanges of goods for money) to match demanded outflows. A monetary system permits net inflows by exchanging new money (or govt securities, we’ll ignore term structure) for goods and services. But it can only do that without coercion or inflation if private agents desire to hold money in preference to goods at conevtional prices. A manager can force balance by refusing to issue new money. She can create net positive flow (negative net redemptions) by running a deficit that private agents accommodate at conventional prices. But if there is a shortfall of gross demand for money relative to gross demand for goods and services at conventional prices, the manager will face net demand for redemptions. If the manager has coercive power, she can try to manage this via taxation: to cover the shortfall, she can create gross demand to exchange goods and services for money (and then confiscate the money). This might or might not work: if the people she taxes already have plenty of money, taxation won’t affect resource flows. Holders of excess money will simply surrender surplus balances. However, if she taxes people who do not hold money, who vastly prefer to hold goods and services than to hold money and have small money balances, taxation can be effective. I guess we could say this in terms of elasticity of real consumption to total wealth: Poor people’s consumption is elastic to total wealth (if you tax them, they use fewer real resources), while rich peoples’ consumption is inelastic to total wealth, so taxing them doesn’t affect real resource flows.
This is pretty different, I think, from the usual Chartalist explanation of taxation as destroying (“uncreating”, winterspeak?) money, even though I think it’s perfectly consistent with Chartalist views. The difference is that I think the monetary authority needs to concentrate on flows, not stocks, that since money balances are notional and insignificant, taxation must be understood and designed to alter flows, i.e. the degree to which private agents will wish to exchange money for real resources at conventional prices.
“Thrown into the sea” is a economist cliché for a simplifying assumption modelers often make about taxes. It annoys the hell out of me when “thrown into the sea” models are used to argue that taxation is harmful (because that precludes the possibility that what governments do with taxes might justify the costs). Nevertheless, it is analytically convenient, because it saves us from having to model the government. It’s not realistic, it’s a thought-experiment-only kind of convention. Realistically, what governments do with the real resources they mobilize is transfer them and use them, in ways that might be more or less productive, and whose productivity might be measurably attributable to government behavior or indirectly enabling of private gains. A bridge might be a financial cost to government if no tolls are exacted, but nevertheless worthwhile, and hardly “thrown into the sea”. But we have no way (in this model) of distinguishing between the state of the world with a bridge and without. We simply imagine a world in which agents can be reasonably productive, and given that, the specifics of what the government does with money doesn’t affect our thinking, so we ignore it. Our model doesn’t rely upon resources bought with new money being “thrown into the sea”, but it does rely upon them being used in some manner less contributive to aggregate growth than direct use by agents who haven’t saturated their desire for consumption. That may or may not be reasonable, and whether it is reasonable probably depends very specifically upon the wealth and circumstances of societies and governments.
I feel like this (like the post) is very discombobulated, but I hope I’ve filled in some of the gaps. Thanks again for the very thoughtful feedback.
January 24th, 2010 at 8:46 pm PST
link
Benign — I have very mixed feelings about modeling. I also have a lot of mixed feelings about empirical work in the social sciences (which despite the label always depends upon some choice of model). I think we are in a position of profound uncertainty when we address almost any interesting question, and there is no methodological silver bullet that can save us. We’ve got to be eclectic, rely upon our judgment, do the best we can with the understanding that reality will kick our asses if we get it wrong, even though there’s no reliable way to get it right.
I view models as parables, analogies, stories. I wouldn’t want to write a model that I can’t explain in words. But while expressing a story in mathematical form doesn’t make it true, as an exercise it can help one think things through and provoke interesting questions as one exams the implications. Sometimes a model’s unexpected implications signals that your mathification has garbled the story you wanted to tell, but sometimes they are genuinely interesting.
I hate when models are used as totems of truth or science. I hate even more when models are used to exclude people from conversations, to claim authority for ones own position while denying others the right to challenge unless they can follow the math. But I do find modeling sometimes to be useful, both as an exercise for myself, and as a means of communicating ideas that sometimes get garbled in the words.
January 24th, 2010 at 8:54 pm PST
link
Matt — I’m perfectly happy to think about a world in which land, labor, capital, whatever are reshuffled and rearranged. That’s really more accurate than imagining “consumption”.
But I think you’ve assumed the answer to what I think is the interesting question, that is who will make the best decisions about how to organize real goods and services. I don’t think that a high savings rate, as conventionally measured in financial terms, necessarily leads to a “productive” or “forward-looking” organization of real resources.
If wealthy people hold financial assets, if in doing so they are more motivated by managing risk than by maximizing return, and if there is a financial asset available that promises by hook or by crook to sustain purchasing power, whose issuer is not good at organizing resources but has confiscatory power to make good on its promise, then “savings” might lead to less rather than more (and worse quality rather than better) uses of real goods and services than would occur if agents had allocated directly. The argument is more complicated when savers purchase corporate stock, but if agents do say based on extrapolations from history and if they blindly diversify rather than carefully allocate resources, then savings in financial assets might also lead to less productive arrangements of reality than more direct use. (See my response to pinus above.)
In the end, this argument depends upon the quality of the financial system. If the quality of the financial system is high relative to the quality of non-financial-system-mediated uses of resources, then by the argument presented, inequality will be good for growth. If the quality of financial-system-mediated uses of resources is low, then more equal economies will grow faster. Even a low quality financial system will be widely used (and will be better to have than nothing), not because it is conducive of growth, but because it provides a means by which agents can pool risks.
January 24th, 2010 at 9:09 pm PST
link
Steve: I am afraid that your answer in [20] only makes things worse. As somebody else pointed out, you assume the answer (rich make socially worse investment decisions than poor), and cook up a model around that. That’s not good but fine, we all try to do various things and learn from them. In [20], you try to make further cumbersome assumptions about how markets are unable to allocate resources that could help save your model. And that’s worse. For instance, your argument:
“diversified portfolios of “risky financial assets” purchased by the wealthy are more like money than real investment”
completely misses the point behind diversified portfolios.
I say – if you are interested in growth and inequality, look for realistic causes. The one you described is clearly rejected by the data, and trying to save it produces worse and worse arguments.
P.S. Just a thought at the end. Let’s take your assumptions a little bit more seriously. If you really assume that rich make worse investments than poor (“But I think that, in fact, for informational reasons and because most projects face diminishing marginal returns beyond a certain scale, wealthy investors are not able to select and discipline financial portfolios as productively as individuals manage their own real investments.”) then in your world, inequality will disappear over time. The small guys will get richer, and the rich guys poorer.
In your model, this might not happen, because you fix the price of the bubble asset (which is clearly unrealistic, and without it the bubble asset will go away), but real-world consequences of your assumptions would be as I described. And then we could just say “Oh, forget the whole inequality crap, it will go away, because the poor can invest better.”
Again, here we can resort to data. And again, the data goes against your assumptions. Evidence clearly (and not surprisingly) shows that poor make worse investment decisions. There are many possible factors, from lower education, over higher relative information cost when managing small portfolios, etc. etc.. But if you want to do serious research in the link between growth and inequality, then this is actually good news for you – it tells you that we cannot expect the capital markets to miraculously close the gap between rich and poor. And this is most likely true.
January 24th, 2010 at 11:45 pm PST
link
SRW 8:46,
Thanks. Makes sense now.
It helps to think of all economic agents as literally being “agent dealers” for the monetary authority, accepting redemptions in exchange for goods and services.
But the net effect of the way you describe the role of the issuer in the issuance/ redemption dynamic seems very compatible with the normal Chartalist explanation. They describe taxation as an adjustment to aggregate demand (as opposed to “funding” anything). But they also describe it as effectively destroying the stock of money (the classic example being that of using currency to pay taxes, currency that is subsequently shredded).
I’m coming to interpret Chartalism as the deliberate prioritizing of a “stock” centric perspective in explaining the functioning of the monetary system. It’s important to Chartalists not to interpret taxation or deficits as “funding” anything, and that the government is not “revenue constrained”. Interestingly, these are income statement interpretations that are rejected. The reason I think is because of the disinformation risk inherent in flow centric rather than stock centric thinking.
Chartalists do not like income statement interpretations of government finance. They like balance sheet interpretations. The reason is that the balance sheet centric explanation liberates a conventional and very inconvenient and erroneous causality bias. Using a stock centric approach, everything becomes an adjustment to the size of the natural net liability position of the consolidated government entity. Both expenditures and taxation are adjustments to a net liability stock. The natural Chartalist order of things is that expenditures expand the stock and taxation shrinks it (as opposed to the conventional order that taxes “fund” expenditures.)
This is pretty consistent with your way of explaining it. Issuance expands the stock. Excess demand for redemptions causes the monetary authority to slow down issuance or to tax. This is VERY consistent with Chartalism, which interprets taxation as monetary policy, through its effect on the size of the net liability. Indeed, fiscal policy becomes monetary policy in Chartalism, and the old mechanism of active interest rate setting is replaced by a structural transformation to zero interest rates (and no bonds) – i.e. your exclusive money model in that sense.
Making the transition from the interpretation of the money dynamic per se to the distribution issues you deal with then seems intuitive. I like the approach of the comparative elasticity of consumption to taxation by wealth category (seems brutal, but effective).
BTW, I pulled up some real slacker economists when I Googled “thrown into the sea”.
:)
January 25th, 2010 at 12:20 am PST
link
pinus — i think we are talking past each other.
“If you really assume that rich make worse investments than poor…” I don’t assume that. I assume that are rational and make identical choices under identical circumstances. Wealthy investors rationally prefer insurance to risky higher returns in my model.
I don’t deny that in the real world, there’s lots of heterogeneity among people, and much inequality is caused by people making better or poorer choices. But that’s not what I’m interested in examining here. In a nutshell, the model says…
“Suppose individuals are rational but risk averse, and that their risk preferences are such that they voluntarily accept lower returns in exchange for shedding risk as their wealth increases. Then, unless the high returns achievable by the very poor are sufficient to overcome the lower returns accepted by the very rich, inequality will lead to slower aggregate growth.”
I am not ignoring evidence: I’m stating assumptions, and I think I’m pretty clear on pointing out that they are assumptions, and different assumptions would lead to different results in both the post and the comments. I think the assumptions are fairly reasonable, but you can dispute them.
If you want to claim that diversified portfolios of financial investments are in fact better investments than the real economic purchases of the poor, that they dominate in terms of both risk and return, and if you don’t dispute the assumption that wealthier people put proportionately more of their funds into financial investments, then you have to make a behavioral assumption or define some friction to explain why rational but poor agents don’t choose the better investment. If you want to claim decreasing relative risk aversion, such that agents in general take on progressively riskier but higher expected yield investments as their wealth increases (and not just within the financial portfolios of the very wealthy, but for agents with few financial investments as well), then my logic inverts, and inequality promotes growth. I actually buy the social insurance story, under which relative risk aversion is not monotonic, so that at very low levels of wealth inequality helps growth because poor people without social insurance are extremely risk averse. But I don’t think there’s evidence that as wealth increases, people generally seek and succeed at finding higher returns than they realize on the real investments they themselves would and perhaps did make at lower levels of wealth. An individual of modest means rationally chooses basic shelter over accumulating financial assets, and that is a higher return choice. The high returns on shelter require people to take on undiversifiable idiosyncratic risk (picking the wrong location in which to live can be very costly), but the returns foregone by choosing homelessness merit that taking risk. The same individual when she already owns a home faces little marginal return and high idiosyncratic risk for incremental home investment, and rationally chooses to accumulate financial assets of moderate yield but low idiosyncratic risk. That’s the story in a nutshell.
I’m perfectly open to the idea that in real life, many poor people simply make poor choices, but that doesn’t invalidate the logic of the model that even if people make identical choices, a rational preference among wealthy agents for lower return financial investments in order to diversify idiosyncratic risk can lead to a drag on aggregate growth. That’s all that I’ve illustrated here, and I certainly stand by that.
January 25th, 2010 at 1:35 am PST
link
Steve-
I think we are on the same page now, per your comments, which is why I do not think your model makes sense. If you think about wealth as the right to allocate capital, than its simply a question of who is best at doing this. No model is necessary.
With that said, I think you may be overrating the importance of financial assets in determining whether inequality is good for growth. To the extent you are talking about savings being funneled into financial assets that have no real value (in some sense, the stock market) but are just paper that people bet on, wealth redistribution should be almost a wash because no claim to real assets is being made. But otherwise, a way to look at savings is this: savings lower the required returns on investment in order for an investment to be made profitably. Where consumers spend or desire to spend in the future (should) determine where investments are made. When more resources are allocated toward future consumption, there should simply be more resources for future consumption. This will, by definition, increase gdp. It may not neccesarily optimize total or depreciated total consumption over the long-term, but it will increase gdp size. And my feeling is that since technological growth is dependent on savings (including pseudo-savings when costs are low but R&D is high, like health care), it will lead to higher consumption levels.
There are other arguments to be made, such as those who have more money tend to have more money because they are better investors, etc. But you can make an argument in any direction at the end of the day.
–
On the other hand, if you believe that the wealthy are using monopoly power to steal money through ‘hook or crook’ well then I agree with you that that is at a minimum morally wrong.
January 25th, 2010 at 2:12 am PST
link
Also, you are making the assumption that the wealthy have a higher level of risk-averseness per $ than poor people, and I don’t see why this must be true. Even if it is true, you must compare the savings rates of rich vs poor to look at absolute expected returns/dollar earned, not expected returns per dollar saved. This is further complicated by the fact that a reasonable shair of consumption can be seen as savings.
January 25th, 2010 at 2:16 am PST
link
Matt — So, I’m not assuming that the wealthy are more risk averse than the poor: all individuals are identical in the model. I am presuming a variety of risk-aversion under which people act as though they are more concerned with return than risk at lower levels of wealth and more concerned about risk than return at higher levels of wealth. I think that’s true (with some exceptions when people lack social insurance so that bankruptcy means death or hunger), but it’s arguable. I also think that the behavior I describe, where the relatively poor find high risk / high return investments and the rich find lower risk, more modest investments have to do with information and opportunity as well as risk: there are ways of “bootstrapping” and multiplying low wealth, while there are fewer ways of multiplying your billions, there are diseconomies of the scale the wealthy must find means of profitably investing. I can mathematically model the risk part, so I emphasize it, but a more complete model would include both.
The crux of the argument has to do with the productivity of the financial investment of the wealthy in an unequal society. My claim is that it is less productive than the real investments of the less wealthy (not all the less wealthy, but as a stylized fact, treating people as identical in all respects other than wealth). I don’t actually believe that full stop: my guess is that much financial investment is very productive, but that eventually an economy exceeds the scope of very productive financial investments, and then financial investment in aggregate becomes less and less efficient, but still the best alternative for the wealthy for whom the insurance value of even low-yield fiat money they never expect to spend is better than nothing.
But for the model, that’s an explicit assumption, and if and when a financial system invests more productively than unmediated real investment, the prediction of the model flips, and inequality is good for growth. I actually think both stories are relevant and sometimes true. (I think at the moment, financial systems around the world are very poorly arranged, though. But that has not been as true always and everywhere.)
I’m not really claiming that the cause of inefficiency in general is theft, although I think it sometimes is. This bears upon the issue of financial savings and investment productivity. As you point out, more financial savings reduces the cost of capital which, ceteris paribus permits more (but less productive!) real projects to go forward. But there is a countervailing effect: if wealthy investors have already endowed their own future consumption, and the poor cannot consume very much, there are no profitable projects to invest in. That is, expected returns on financial investment are also impacted by wealth distribution. This is in the model a little, although in a way that really calls out the fact that financial/nonfinancial isn’t really the right distinction, it’s to what degree investment/consumption is real-economy-productive or not. By construction I make financial investment nonproductive in the model, but a better model would have a range of more or less productive investment choices, rather than “bad money, good real expenditure”. Anyway, in the model, people are claimed to endow their own furture consumption with their spending. That might mean banding together and purchasing factories at scale, which in practice would mean financial arrangements, but would exclude zero-yield money. Since, at equality, all agents seek to endow their own consumption, there is no issue that wealthy agents would lack useful projects because their own consumption needs are met (at some level of wealth, they prefer more insurance to more consumption at the margin). Under inequality, many profitable projects in terms of “aggregate utility” are financially unprofitable, because potential consumers haven’t the wealth to purchase the goods. So there’s a catch 22 where the wealthy seek profitable projects, but can’t find them, although there are projects that in some nonfinancial sense would improve aggregate outcomes. In this situation, the interest rate gets low (plenty of savings!) but all projects look crappy, because potential demand is poorly matched to purchasing power.
January 25th, 2010 at 3:27 am PST
link
IA — Don’t imagine that because under the very stylized assumptions of my model a monetary Ponzi scheme can be stable means that I think existing real monetary Ponzi schemes will be stable. (By revealed portfolio preference, you know I have my doubts.)
Part of what’s nice about the model is by showing how a monetary Ponzi scheme might be stable, it helps think about under what circumstances it might not. To wit, according to the reasoning in the post, such a scheme might be stable if i) there is only one candidate risk-free asset; ii) investment returns are positive on average and uncorrelated, so that in aggregate the population always has stuff it wants to trade for money rather than trying to trade he money it already has for stuff. If either of those conditions fail, especially if there is a period of widespread investment losses that cause people to try to fall back on their precautionary savings, the Ponzi is expected to fail. If it does fail, outstanding money balances, that is the quantity of greenbacks and government debt the public thinks it holds, is likely to affect the degree of devaluation or inflation (or taxation of the not-rich) that would be required to restore a balance of flows. Too much past-printed money suggests a larger devaluation of the money.
But first and foremost, what I’ve learned from this exercise, is it’s all about flows. As long as people are willing to trade stuff for money at conventional prices, the system is stable. The catalyst for a change will be when people in aggregate demand some kind of stuff that is in scarce supply. Then (and perhaps quite suddenly) the outstanding money stock may become ammunition for a bidding war, leading to a jump in prices.
If the stuff demanded is human labor, that’s when a general inflation really kicks in. But that seems unlikely for the moment. If the stuff demanded is a commodity, then maybe the government doesn’t print a high inflation statistic; it just looks like copper is expensive or something.
January 25th, 2010 at 6:14 am PST
link
OK, back to my suggestion of Dinuba and Arvin as empirical examples. This sort of modeling can be used toward an explanation of the effects of very real interventions. The tour begins with preference for the distribution of water for irrigation to small scale farms, moving toward the preference of accumulated wealth to look to productivity in their own terms as the financialized version of ROI. The impact of a chartalist influence on the distribution of funds can also affect the distribution of that social institution established to facilitate exchange (ie “money”), as well as the potential effects of cutting out of the process of the agency intervention in the re-distribution of “money,” as well as the potential effects of the elimination of the fractional reserve/leveraging franchise, to illustrate the multiplier effect within relatively leveled communities versus company/mill towns, and further the leveling likely under a Georgist process of taxation versus not.
The use of Chartalism as a explanatory model of monetary institutions and sovereignty hinges on its higher level of power of prediction as opposed to the micro-economic fantasies used to validate macro-economic effects. As an example Wray’s chartalism is in some need of translation at times, and this sort of modeling would aid its rhetoric.
On modeling more generally, as long as it is used as a tool toward illustration and not as a totem connoting a special status, then it is just another problem solving tool. AND there are complex issues that exceed easy expression. To use McCloskey’s perspective it is a form of rhetoric, nothing more and nothing less. The hijacking of the Hemholtz equations was a dark ages digression into positivism as an article of faith, rather than supposition. Of course most of the econo-modellers seem to be entranced by the Gee Whiz and the supposed status conferred, and the dialectical advocates have generally demeaned the whole utility as intrinsically toxic. Of course the scale also matters, where in general national economies are treated in more of a black box process via sociometrics. Accepting that the middle and micro range processes will vary from context to context doesn’t eliminate the point of entry for an analysis, of course treating the macro level as the primary level of analysis, will end up obscuring the real effects, eg the basic stupidity of using the GDP as the sole measure of “growth,” and thereby used to imply sustainability. The partitioning of economic patterns also has real effects, that can also be reflective in a interpolating sense.
more as we go, Tadit Anderson
January 26th, 2010 at 11:55 am PST
link
Is there any way that you can change my website url, I don’t see an “edit” option. It should be Re-Imagining Economics at http://www.economics.arawakcity.org (I accidentally dropped the “s” on economic(s) Tadit
[Done. —Steve]
January 26th, 2010 at 11:59 am PST
link
On Ponzis One of the interesting pieces about Hyman Minsky’s “Stabilizing An Unstable Economy” is that he uses Ponzi as an analytical tool, not necessarily as category of criminal behavior. There several governmental funds/operations that perform in a Ponzi way, in terms of the out flow has to balanced against the inflows. It is where the two different aspects become imbalanced toward draining the expectations of out flow that the process will crash. The same analytic also works for ordinary businesses. The aspect of criminality arrives when the processes are not transparent. The chartalist notions of taxation and expenditures is one version. Lunatic non-profits who depend upon financial illiteracy to avoid transparency and accountability can end up as primarily a executive employment ponzi accomplishing little otherwise in terms of its declared “good intentions,” the non-profit analog of predicted high rates of return more commonly used by Madoff and his brethern to rip off the already greedy. In effect the ponzi is a “chartalist” analytic. Tadit
January 26th, 2010 at 12:13 pm PST
link
Steve,
In relation to your comment #34.
1) Such a ponzi flow model makes asset prices pretty much garbage for making rational economic decisions. Though I believe you already covered this in other posts.
2) Linked above, this can cause people to think they have more capital then they really do. Since economic decision making uses profit/loss to inform choices ignorance of appreciation/depreciation makes such a calculation difficult. Someone can be engaging in economic activity they think is possible because they have little pieces of paper coming in but in reality those little pieces of paper don’t represent real capital. Their monetary flow indicates profit but that isn’t occurring on a societal scale.
3) As you note when people try to use their savings to buy real goods the entire thing blows up, which is exactly what will happen as society ages and baby boomers move from saving to spending their “assets”.
January 27th, 2010 at 12:48 pm PST
link