Hidden profits, hidden rents
Evan Soltas has a very good post on the explosive growth of the financial industry since the end of World War II. As a share of GDP, in terms of profits, and in terms of payroll, postwar America has been truly been a golden age for bankers, brokers, and fund managers.
In fact, it’s even better than it looks!
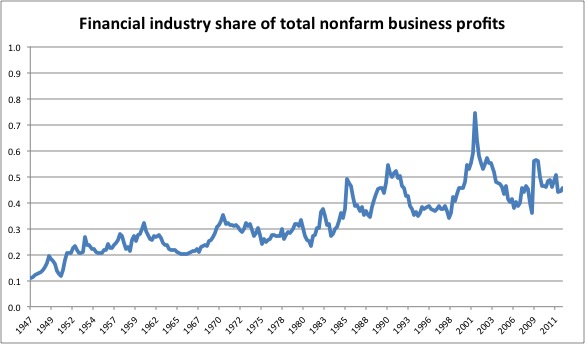
Soltas begins with a graph:
The graph above shows that the financial industry now makes roughly half of all nonfarm corporate profits in the U.S., a share which has risen five-fold since the end of World War II.
“Profit” is always something of a sticky subject. We talk about it all the time, like we have any idea what it means. Usually we don’t. There is, for example, the distinction between “accounting profit” and “economic profit”. Accounting profit is what a firm, under generally accepted accounting principles, can claim to be the earnings that accrue to shareholders. Economic profit is revenue that exceeds the true cost, defined as the value of the next-best opportunity, of all inputs. According to theory, in a competitive market, economic profits should be relentlessly pushed toward zero while accounting profits should stay positive but very near the broad market return on capital placed at comparable risk.
In general, only accounting profit is measured while only economic profit is interesting. When we think of economic profit, we need not restrict ourselves to shareholders, who represent just one class of claimants on an enterprise. Suppose there is an industry whose firms about break even in accounting terms, but whose unionized workers, even those without hard-to-find skills, capture salaries much larger than they likely would outside of the industry. Is the industry “profitable”?
In an economic sense, it is very profitable. It generates sales that far exceed the opportunity cost of its inputs. But for institutional reasons, those profits are captured by workers rather than accruing to equityholders, and so are missed by accounting measures. It’s pretty clear that, in its heyday, the US auto industry was like this. The industry generated a great deal more “value” than was captured by its shareholders. The internal negotiations between firm stakeholders over the distribution of economic profit has no bearing on the existence of that profit.
The financial industry is not heavily unionized, but the lack of a union doesn’t mean the struggle over the distribution of economic profit goes away, with shareholders automatically winning. In many industries, economic profit is far higher than accounting profit, with the difference captured by various sorts of insiders. And there is no industry in which the distribution of economic profit to employees is more institutionalized than in finance, where at large banks roughly half of firm revenue get distributed to employees, largely in the form of bonuses. Now, one can argue that the form in which compensation contracts are negotiated says little about whether the level of that compensation exceeds the opportunity cost of the work to recipients. Perhaps bank employees earn higher salaries on average than they could elsewhere as compensation for the bearing much of the risk of firm performance by accepting low base salaries and uncertain bonuses. But.
Economic profit creates an incentive for new entrants. Indeed, given how difficult it often is to measure the true cost of inputs, the best way to observe economic profit is to look for people banging at the door. And people do seem to be banging on the door in finance. Famously large fractions of Ivy league graduates — who can do anything, for whom “the world is their oyster” — end up taking finance jobs, despite very often having no specialized training in the field. I hope it will be uncontroversial to suggest that finance jobs are coveted. Those low base salaries delivered with a variable upside are, it turns out, not so low when compared with salaries in other industries. It is true that much of the “economic profit” earned by bank employees is delivered as a claim on a high-mean-value probability distribution rather than as a certain paycheck. But the opportunity cost of the input is mostly covered by the base. [1]
To the degree that financial firms’ economic profit is unusually captured by employees rather than shareholders, accounting-based estimates of finance’s profit share, like the one that Soltas presents above, will badly underestimate the share of economic profit captured by finance industry stakeholders as a whole. [2]
That an industry captures a lot of economic profit need not be a bad thing. After all, economic profit represents “value added”, the degree to which outputs are worth much more to people than inputs. However, we often divide economic profit into two components, the usually-transient good kind that results from innovations which leave firms a step ahead of their competition, and bad “rents” that result from capturing subsidies and/or restricting competition. To be fair, most successful firms get some of their economic profit both ways. But you’d need a great deal of faith in empirically invisible new value to explain the persistent and growing profit captured by finance, if its source isn’t predominantly rents. And, indeed, Soltas enumerates some of those:
Let’s run though the explicit subsidies: the mortgage-interest deduction and other homebuyer credits, student loan aid, federal guarantees on debt, the preferential tax rates on capital gains and dividends, interest on reserves at the Fed, and the FDIC guarantee. The financial industry also benefits from substantial implicit regulatory subsidies such as “too-big-too-fail.”
That’s a very good list. I’d add one more: the Federal Reserve’s policy of stabilizing the purchasing power of currency. Though stock markets and fancy derivatives get lots of press, most of the abnormal profits in finance are, I think, earned in debt markets. Financial firms borrow money and lend money. They underwrite debt issued by others and structure that borrow and lend. Financial rents seem related to scale and concentration. Debt-based financial intermediation is amenable to economies of scale in ways that equity-based funding is not. Rating agencies can get away with classifying debt products like beef, USDA Triple-A, and trillions of investment dollars flow accordingly. Investors are more idiosyncratic and more cautious with equities. “Too big to fail” is primarily a quality of credit markets — no one thinks that any bank is too big to suffer a stock-price decline. When financial firms extract rents via explicit government support, it is usually in order to ensure that bank creditors are made whole.
But debt finance exists in competition with equity finance. If I’m right that debt finance is a more fertile source of industry rents than equity, then ways that the state tilts the scale towards debt funding are part of the problem. Along with Felix Salmon, James Surowiecki, and many others, I’ve argued against the bias towards debt embedded in the tax system. But stabilizing prices also increases the relative attractiveness of debt. Absent price-level stabilization, the business cycle risk borne by diversified equity investors is somewhat counterbalanced by reduced risk from inflation, as price increases pass through to earnings and dividends over the medium term. If recessions tended to be inflationary, as they would for example under an NGDP target, this pass-through would amount to a very desirable countercyclical feature. Debt, on the other hand, would lose value in real terms during inflationary recessions. (For lower quality debt this loss would be partially offset by reduced risk of default.) The current practice of targeting inflation makes default-risk-free debt a nearly no-lose proposition regardless of macroeconomic performance, while accentuating the exposure of equities to business cycle risk.
There are lots of good reasons to reduce our dependence on the institution of debt in favor of more equity-like arrangements. Evolving towards a smaller financial industry less capable of capturing rents is another reason. Using the power of the state to stabilize the inflation rate is a bad idea, also for lots of reasons, including that the practice encourages debt finance and powerful banks.
[1] Even to the degree that supernormal paychecks are compensation for risk-bearing, part of the compensation should be recategorized as a return on shadow equity, rather than as a cost of labor input. One can decompose a bankers’ variable compensation into a cash payment plus funds that might have been paid but are instead invested on the employee’s behalf into the firm or a subdivision thereof. Much of bankers’ bonuses, the part that is compensation for bearing firm risk rather than paying for labor, should be viewed as a return on shadow equity that doesn’t show up in the formal equity accounts. When banks recruit employees to finance the firm with deferred compensation and then pay a performance-based return on that advance, it is quite similar to issuing new shares or outcome-contingent securities. The return eventually paid on those securities in excess of the original amount deferred ought to be considered distributed profit rather than labor compensation.
To highlight the murkiness of the dividing line between compensation and profit, consider two employees. One employee is paid at the beginning of the year in the form of firm stock, which will not “vest” (be made available) until the end of the year. The other is paid 20% less, but gets conventional cash payments and will receive an end-of-year bonus based on firm performance. Suppose the firm’s stock rises by 10% over the year, and our cash-paid employee receives a bonus worth 40% of her base salary. If you do the math, you’ll find that the cost to the firm of the two employees is almost the same. Both employees bore similar (although not identical) risk. Yet on the books, the first employee’s compensation will be smaller than that of the second employee, with the difference reflected in the earnings of the firm. Rewriting the first employees explicitly equity-based contract into a reduced-compensation-plus-bonus contract changes little of substance, but reduces the firm’s accounting profit (and tax basis!). Since compensation-plus-bonus is common in financial firms, reported profits are low relative to an world in which the variable basis for the compensation was recorded as equity. Yet recording the compensation as equity more accurately captures the division between compensation for labor and the compensation for risk-bearing that defines accounting profit.
Note that this analysis is unchanged if the motivation for the variable payment is to encourage performance, and is based on outcomes close to the employee, rather than firm-level performance. The employee is then compensated in equity in smaller, riskier subdivisions of the firm (and might require a higher salary “in stock” to compensate), but that does not alter the opportunity cost of her own employment or the fact that proceeds from good outcomes represent economic profit.
[2] Finance is unusual but not unique — see also health care, education, and government, together the “information asymmetry industry“.

[…] You may not realize the magnitude of the banks' post-WWII dominance over this country. (Interfluidity) […]
February 27th, 2013 at 7:38 am PST
link
But debt finance exists in competition with equity finance. If I’m right that debt finance is a more fertile source of industry rents than equity, then ways that the state tilts the scale towards debt funding are part of the problem. Along with Felix Salmon, James Surowiecki, and many others, I’ve argued against the bias towards debt embedded in the tax system. But stabilizing prices also increases the relative attractiveness of debt. The current practice of targeting inflation makes default-risk-free debt a nearly no-lose proposition regardless of macroeconomic performance, while accentuating the exposure of equities to business cycle risk.
——————————————————————————–
Sir, you have old people that want safe investments on which they can’t lose, and the politicians and financial industry in cahoots to offer just that with the bailout costs and subsidies that implies. And you have full employment for technocrats like yourself and Bernanke who think they can regulate the issue. Which is impossible.
February 27th, 2013 at 7:48 am PST
link
Two key points here. And both can be related to inequality. The changing structure of economic profits, away from large scale manufacturing where workers with a low level of education can capture a share and toward the financial industry where a higher level of education is required is a key driver of growing inequality. Second regardless of debt or equity as a means of financing business the changes in tax policy, reduction in marginal rates and lower capital gains taxes have increased the demand for any type of securities. Arguably the velocity of security transactions has increased. This grows the financial industry and enhance profit making opportunities. It’s not clear how much of this market is about efficient capital allocation as opposed to simply satisfying the demand for investment products which are actively traded.
February 27th, 2013 at 11:20 am PST
link
This is idiotic. How would an NGDP target be achieved? Whatever your answer is to that question is what you should say instead of saying that an NGDP target would cause inflation. SHEESH
February 27th, 2013 at 2:48 pm PST
link
What makes you think half of revenue goes to compensation “largely in the form of bonuses”? If you look at JPM’s number it’s more like a *third* within the investment-bank segment. It was 32% for the company as a whole in 2012. Come to think of it, “vanilla” retail banks might pay out more, if that’s the way you want to look at it. Spot-checking this now, Fifth Third is at like 30%. No biggie.
In fact, if you look at the different business lines, JPM’s trading operations are much more profitable for *shareholders* than their retail banking. Are we then to conclude that tellers are being overpaid and big-shot traders underpaid? Well, maybe…
February 27th, 2013 at 9:40 pm PST
link
Also, surely it’s worth pointing out the *other* side of government participation in banking etc.? Is there any other industry with more overlapping and detailed and costly regulation? The CEO of a small Michigan bank that was recently acquired once talked about how she knew she needed to link up with a bigger firm when she realize that she had to hire 5 more risk management/compliance employees to handle new Dodd-Frank rules. For someone like JPM, hiring 5 people is not a big deal; for her, because they would be high-salaried technocrat types, it would be a really substantial drag on profitability that she couldn’t afford. (It’s pretty well accepted in banking circles that the only way to survive the new regulatory climate is to gain more scale. This doesn’t mean that regulations are bad, but there is a very natural tension between the regulatory anti-subsidy and the fearof banks getting too big forever, which I don’t see anyone really acknowledging, even though it’s very real and happening today.)
Maybe this sort of thing doesn’t outweigh the benefits cited (although some of those accrue to e.g. borrowers, not financial firms), but it’s far from obvious to me how the scales really balance. Certainly there are a zillion bankers who would tell you that they’d much prefer to forego the claimed benefits if they could get rid of some of the shackles. They could well be deluded, but their viewpoint deserves consideration if you’re trying to get the facts right.
February 27th, 2013 at 10:02 pm PST
link
[…] Hidden profits, hidden rents – Interfluidity […]
February 28th, 2013 at 3:03 am PST
link
Aside from top management, I just don’t see how it is plausible that bank employees in general have the leverage to collect rents from shareholders. Bank management has every financial incentive to minimize the pay of rank-and-file employees.
February 28th, 2013 at 4:06 am PST
link
@Richard,
what you write is true about classical retail banking – but then it’s true just about any management-run company.
In IB, it’s quite usual that “star” performers (read those who generate the largest transactions, trade profits etc.) are paid MORE than the C-suite, sometimes more than the C-suite combined. The money go where the power is, and the conventional wisdom is that he power is with the stars. Personally, while really good salesperson can add a lot, usually there’s quite a bit of beta going on – that is, the gains achieved by the virtue of the organization (cheap funding, credibility to large clients, large BO dealing with regulators etc. etc.) which the same people could not hope to achieve on their own (which is the reason why they don’t run their own companies, and often fail when they go out and start their hedge funds for example).
But, as is always the case, distinguishing between beta and alpha is hard, especially when the part in the question has no incentive for it (or incentive for muddling it up).
February 28th, 2013 at 5:44 am PST
link
@vlade
It may be that star performers are overpaid for the reasons you say, but this doesn’t sound like a rent-extraction story — just poor judgement on the part of managers. Also Steven’s post implied that the high salaries of fresh graduates headed for Wall Street are somehow explained by rent extraction, but I find it entirely implausible that these employees have the leverage to obtain above-market pay.
It is entirely likely that part of banks’ economic profits are derived from rents. My assertion is that the way the pie is split between shareholders and employees is determined primarily by normal considerations of bargaining power (with the likely exception of top managers — but this is the case in all industries).
February 28th, 2013 at 7:57 am PST
link
And that’s it in a nutshell. Clinton bent the knee to Greenspan as policymakers allowed an unregulated (and yet backstopped) shadow banking system to arise. All for campaign contributions? We need a social democratic party that will domesticate the financial sector and go Shinzo Abe on the FOMC.
February 28th, 2013 at 11:42 am PST
link
nice ost
too long for a sub vocalic reader eager to comment however
i lie to see the hi fi sector as an unofficial rent extractor
along the lines of a “state” trying to find the sweet spot
outlined in greenwald stiglitz
optimal taxer optimal extractor
my point if any
don’t call this extraction a profit stream
at least not anymore then u’d call
a tax on ground rent a profit stream
February 28th, 2013 at 2:10 pm PST
link
If, as a matter of commie fighting, you allow multiple nations to peg their currency to yours, then you need to be prepared to invest all the capital created by the pegs. It would be unreasonable to expect them to put the currency in their mattresses.
February 28th, 2013 at 2:14 pm PST
link
are you familiar with a rudolf meidner tax ?
the failure to implement this beuatiful tax
pretty well ended the swedish dash toward eden
at least by way of tax and transfer systems
under the paine soviet system
the commanding heights would operate with similar isle of Laputo savagery toward the underlying production archipeligo
difference
the extractions would get tossed in the general social surplus melder
February 28th, 2013 at 2:16 pm PST
link
“There are lots of good reasons to reduce our dependence on the institution of debt in favor of more equity-like arrangements.”
this amounts to finance sector trog thought
worthy of time spans of petite bourgeois reformers
from minsky back to sismondi and beyond
probably back to Crassus in our occidental cultural frame work
February 28th, 2013 at 2:33 pm PST
link
@Richard
Where do you see SRW saying that the employees are extracting rents from shareholders? I’m not saying it isn’t there, I just must have missed it.
February 28th, 2013 at 4:03 pm PST
link
[…] trap? (MarketWatch) • The Rise of Finance (Ecan Soltas) see also Hidden profits, hidden rents (interfluidity) • Personal finance media should be boring (Abnormal Returns) • Eisinger: A Revolving Door in […]
February 28th, 2013 at 4:30 pm PST
link
Steve,
While there is no doubt that the FIRE sector is out of control, the data you rely upon don’t actually tell us anything about the FIRE sector’s share of GDP.
Why?
Because GDP is domestic and “domestic” corporate profit data are worldwide. See this from the BEA:
http://www.bea.gov/scb/pdf/2011/03%20march/0311_profits.pdf
As the document shows, the BEA’s NIPA “Domestic” Corporate Profits data measure profits earned worldwide by companies headquartered in the U.S. Thus, for example, the FIRE sector’s share of “domestic corporate profits” says nothing about the FIRE sector’s share of “gross domestic product,” i.e., nothing about the U.S. economy, real or otherwise.
What would we find if domestic corporate profits were limited to profits actually earned by a “US headquartered” company in the US? What would we find if looked at all profits earned in the US by all companies, foreign and domestic?
I don’t know the answer to those questions, but I imagine they would be far more frightening and profound than what you get when you wrongly assume that profits earned outside of the US and not taxed by the US says anything about a company’s “share” of US GDP.
March 1st, 2013 at 12:11 am PST
link
Steve,
Check out the article in Mark’s links from a former high level trader:
http://blogs.scientificamerican.com/guest-blog/2013/02/27/why-its-smart-to-be-reckless-on-wall-street/
It’s off the hook good!
When you actually work inside, you can learn and understand so much that an economist from the outside never could. You learn the intricate details day by day, every day, all day. You live it, and the strategy and the people. I found the same thing in my youth working as an auto insurance brokerage agent/salesman (and in other sales jobs). It really taught me a lot about salespeople and consumers and brokerages that it would have been hard to really learn from the outside.
March 1st, 2013 at 12:14 am PST
link
“But for institutional reasons, those profits are captured by workers rather than accruing to equityholders, and so are missed by accounting measures.”
Good point! Huge, when it comes to our out of control rapacious finance traders and managers. I shudder to think what that graph would look like if that was included.
March 1st, 2013 at 12:42 am PST
link
[…] rise of finance (Evan Soltas); and Hidden profits, hidden rents (Interfluidity) [Finance has grown to make up roughly half of all nonfarm profits in the […]
March 1st, 2013 at 4:48 am PST
link
Usually in economics hidden rents and profits are a healthy factors. So no need of worrying too much.
March 1st, 2013 at 5:17 am PST
link
Great post! To me the best way to make sure that debt financing is competing fair and square with equity financing would be to replace current taxes with a tax on GROSS asset values. Then expansion of financial assets would only make financial sense if it led to improvements in underlying productivity. It would no longer be an effective way to play the system.
March 1st, 2013 at 5:17 am PST
link
Just a few notes:
a) The Wall Street firms need to pay a high salary to capture “the best” of everything, not because they need the best in order to do their business but because it is a strong signal that allows them to capture high rents from their clients. We only hire the best. We pay them lots of money. Our services are very valuable.
This signaling is very important in the business as the products are usually either 1)So bog-standard you need to signal a high value despite them not having it or 2) So complicated the client doesn’t really understand them and relies on the signaling value of the company as to the quality of the product.
Think of the high salaries and the “premium” recruiting as investment into Brand that can be levied by the company to extract rents.
There is also a signaling value in paying a few employees incredibly high salaries, much higher than the risk they assume is worth them getting paid.
b) Amongst the employees themselves it is constantly a competition of who can do marginally better as most trades work on a winner-take-all basis. At the same time there are reputational advantages in the business you are doing, in which the winner of the last round gets more clients in the hope that he will win this round as well and more support because he did so well previously, regardless of the what the reason was the did well. This flow of money towards the marginally better employees creates a system of rent-seeking for the individual employees as well.
Now you could argue that this is great because it encourages people to be marginally better, but the problem arises in people being extraordinarily rewarded for a very ordinary marginal improvement, which in most cases comes down to luck, nepotism, insider trading, or happenstance.
The prices the firms offered could be a lot lower if there wasn’t rent-seeking within the industry, and the risks a lot smaller if traders were not encouraged to rent-seek.
March 1st, 2013 at 11:25 am PST
link
[…] See full story on interfluidity.com […]
March 1st, 2013 at 2:08 pm PST
link
[…] On the stunning rise of the financial sector since WWII. (Interfluidity) […]
March 2nd, 2013 at 8:52 am PST
link
A thought-provoking post spoiled by your prejudice against sound money. The Fed’s policy of stabilising the purchasing power of currency cannot be a subsidy to debt finance, because it makes no external input. You might be right that it makes owning debt more attractive, but since there is no subsidy involved, that attractiveness results in returns on fixed income being typically lower than returns on equity. The Fed just sets the environment – stable money – in which fund suppliers and fund users are free to bargain the terms of their transactions. If counterparties valued the existing framework, they might simply reproduce it using index-linked debt if NGDP targeting shifted the framework.
March 2nd, 2013 at 5:13 pm PST
link
As an economy grows and wealth is created, the financial industry has to hire and retain talent to manage and reallocate that wealth. It would be foolish to claim that a certain segment of the labor force is vast overvalued. Overvalued relative to who? The market dictates compensation. When banks reduce compensation, productive employees quickly move to another company willing to pay them more – typically hedge funds. CEO’s with newly accumulated wealth in turn become VC/PE and i/bankers as well (i.e. like me!).
March 2nd, 2013 at 6:53 pm PST
link
[…] in the financial sector because bankers were able to extract a huge amount of the surplus from the activities of banks. Realigning incentives so that banks can control their employees and run more safely is in […]
March 3rd, 2013 at 6:54 am PST
link
[…] in the financial sector because bankers were able to extract a huge amount of the surplus from the activities of banks. Realigning incentives so that banks can control their employees and run more safely is in […]
March 4th, 2013 at 5:57 am PST
link
[…] Waldman zwrócił uwagę na dwa podstawowe źródła generowania […]
March 5th, 2013 at 2:50 am PST
link
[…] aveva il 10-15% dei profitti totali, ma dagli anni ’90 oscilla intorno al 50%… banche, assicurazioni, broker e fondi e altre società finanziarie si beccano ora metà dei profitti. La rendita e l’intermediazione finanziaria dominano. Poi ovviamente ci sono i grandi […]
March 8th, 2013 at 11:10 pm PST
link
[…] […]
March 9th, 2013 at 3:46 am PST
link