Spreads and paradoxical liquidity
In my previous post, I suggested that “depth-weighted spreads” ought to serve as a measure of the uncertainty surrounding a asset’s future cash-flows. Felix Salmon quite correctly points out that quoted bid-ask spreads don’t in fact correlate very well at all with cash-flow uncertainty. Felix notes that the popular stocks often trade with one-penny bid/ask spreads, while you’d see much wider quotations on the more predictable bonds of the very same enterprises. So, what’s going on?
I’ll tell the story in pictures. Don’t be fooled though. Despite the presence of graphs, there is nothing scientific about this exercise. I’m trying to illustrate stylized facts as I understand them, not provide new evidence in support. If you think I’m wrong, let me know.
At about noon today, I took a snapshot of the limit order book for Coca-Cola stock (as presented via my brokers’ trading tool). The “quoted spread” was one penny, bid price $58.10, ask price $58.11. At the same time, I found a Coca Cola corporate bond for which a spread was quoted. The quoted spread on the bond was much larger by any measure: You could sell a bond for $1043.34, or buy one for $1058.85, for a quoted bid-ask spread of $15.42. One penny for uncertain equity vs $15 bucks for a bond whose cash flows are virtually guaranteed!
Obviously, this is not an apples to apples comparison, just given the face values of the bonds. It’s not surprising that you have to pay a market-maker more to take on $1000 of inventory risk rather than $60. (Remember, market-makers are “in the moving, not the storage business”. Their nightmare is that they buy something whose price moves against them before they can sell. You gotta pay them more to take a big risk than a small risk.) But, in per-dollar terms, the spread on one bond is still much higher than that one share of stock. You’d have to pay roughly two basis points (0.02%) in spread on every dollar invested in order to buy and resell a share of stock. To take a round trip on a bond, you’d pay almost 147 basis points! 2 basis points vs 147! So, stocks spreads are much smaller than bond spreads any way you cut it, right?
Wrong. The graphs below shows “half spreads”, the difference you’d pay from the current midpoint price to buy or sell the security according published price quotes. Here’s our view of the world so far:
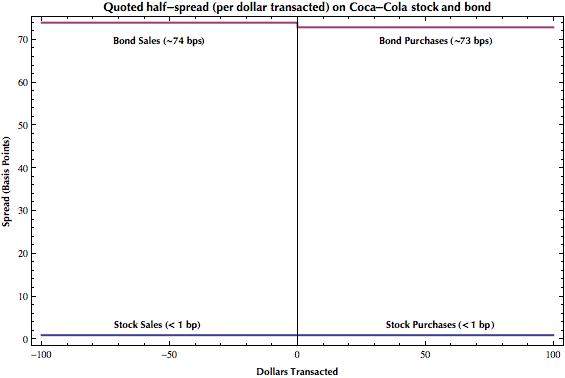
But let’s broaden our horizons, shall we? What if we want to invest, say, $15,000 in Coca-Cola? Is the spread still cheaper on stock?
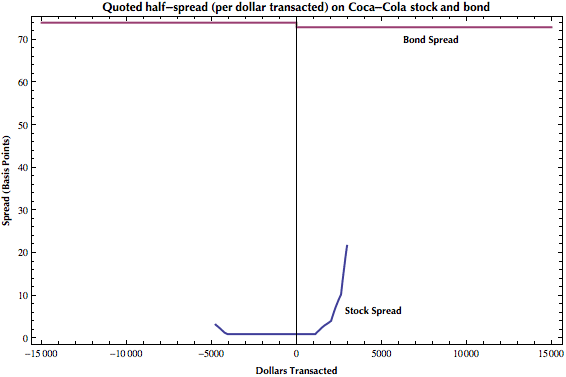
Probably not. Note how even very large, popular stocks are not quoted very deeply, even though the apparent spreads are very small. And note the shape of the cost curve: The cost on a per-dollar transacted basis always increases, and at an increasing rate. (Spread is a convex function of volume.) It’s obvious that if you were to extrapolate on the buy-side, you’d end up paying more for the stock than the near constant, 73 basis point bond spread that would lock in $15K worth of the bond. The quoted spreads on the stock are very narrow. But the price action is a bitch, if you want to transact quickly and in quantity. (Note the asymmetry of the curve. The obvious conjecture is that market-makers are net short, and would prefer to hedge by purchasing than to go shorter by selling. But at some point not very distant from the midpoint, the spread would take off on the bid side as well.)
Here’s an entirely fabricated, but probably more informative picture:
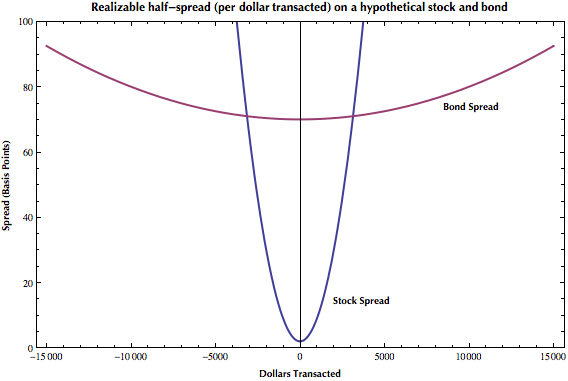
Which security has tighter spreads, the stock or the bond? For small volumes, the stock wins. But as volume increases, the stock’s spread increases much faster than the bond’s, reflecting the bond’s greater certainty of valuation.
Now, again, this is all terribly stylized. Limit order books are notoriously incomplete, and give little hint as to either market supply and demand or market-maker willingness to transact. Actual transactions often occur inside of spreads. Quoted spreads do correlate with various “liquidity measures”, but they are terribly noisy because they ignore depth, and the informativeness of a spread increases with depth. Also, lots of trading happens inside quoted spreads. Volume-weighted “effective” or “realized” spreads, that compare actual transaction costs to spread midpoints would be more informative.
But still. A market-maker in Coca-Cola bonds this morning had written the entire world a free option to buy $74,000 or to sell $18,000 worth of a bond at will. Stock dealers, on the other hand, put less than $5K on the line in either direction. The bond dealer’s spread reflected a less precise but far more confident estimate of the bond’s value.
The shallow, tight spreads on uncertain stock valuations are what I think of as “paradoxical liquidity”. Why do market-makers guesstimate very precise values for (some) stocks, while signaling “no confidence” by putting little money behind their guesses? Why do bond dealers offer looser estimates, but back them with a willingness to trade at high volume? Perhaps bond market-makers face higher fixed costs, limiting how tight they can pull spreads and still be profitable. Perhaps it is because stocks trade in less fragmented, more competitive markets. Competition forces market-makers to converge upon a single midpoint price (however arbitrary), and drives spreads towards zero. But as spreads approach zero, so does profit. Some stocks have penny spreads and other stocks don’t. How come market-makers stick around to drive spreads down to nothing for some equities, but not for others? Is it because low spread stocks can be more precisely valued than other stocks? Absolutely not. As Felix mentioned, even glamour tech stocks, whose prices rise and fall like soap opera divas, sometimes have one penny spreads.
Instead, it is active randomness rather than staid certainty that drives some stock spreads to be much tighter than bonds or shares of less popular firms. Market-makers derive profit from “noise traders”, from people buying or selling at market prices for their own reasons, but who have no better insight into the future value of the stock than the market-makers themselves. When dealers trade with investors who are better informed than they are, they lose money on average. To make up for this, market-makers seek out the business of “fools” (as Tyler Cowen put it, reminding us of the seminal paper by Glosten and Milgrom and inspiring Felix to coin a memorable phrase). Stocks popular with noise-traders attract multiple dealers, who compete spreads down to minimal levels, and then share slivers of profitable foolishness. In the academic model, fools and informed traders are indistinguishable to market-makers, so market-makers must keep spreads wide enough to offset their losses to insiders. But that needn’t be the case. Those making markets in stocks popular with noise-traders could instead try to separate clienteles based on order size, flow, and type. During “lulls”, dealer competition forces prices to converge to arbitrary values at minimal spreads. Dealers collect pennies on small trades as “fools” trade back and forth at market. But as soon as they catch the slightest whiff of informed trading — large order sizes, inventory build-up, rumor, whatever — market-makers ramp up spreads and shift prices until they find a new price point that is somewhere inside of more informed traders lack-of-confidence interval. They then compete spreads back down to an arbitrary price point, and return to happily collecting pennies. The particular price at which a stock trades, despite microscopic spreads, contains little information about the “true value” of the security, other than that the price is “close enough” so as not to draw the attention of informed predators.
“Paradoxical liquidity” is why I suggested in the previous post that “depth-weighted spreads”, rather than simple bid-ask quotes, ought correlate with valuation uncertainty. As quantities in a limit order book go towards zero, Newtonian finance gives way to the quantum spookiness and game theory. In general, we should treat spreads with more money behind them as more informative than those with less, and compare the relative valuation uncertainty of different instruments using high dollar spreads, rather than best-bid-and-ask. But even scale is arbitrary, and noise trading isn’t just about little tech-stock speculators. Another word for noise trader is “liquidity trader”. People who sell at market prices because they want cash, or buy at market because they want a place to park cash for yield, but who don’t analyze the hold-to-maturity value of the assets they swap are, from market-makers’ perspective, no different than sweaty day traders. When, for whatever reason, liquidity traders go away, market-makers find they have no pennies to compete for, and spreads revert to bounds that reflecting valuation uncertainty of people actually willing to bear the risk of ownership. Paradoxical liquidity is fun while it lasts, and consoles naive traders by offering visibly tight spreads in exchange for hidden price volatility. But in the end it serves no one but the middleman. When it “dries up”, withdrawal can be a bitch.
Update: I’ve struck the last couple of sentences. It’s always fun to end stuff with a punch, but I’m not sure it’s right that paradoxical liquidity “serves no one but the middleman”. The shape of the spread curve is probably not something to get too moralistic about. There are positives and negatives associated with what I’ve called paradoxical liquidity. As always, trader beware.
- 7-May-2008, 11:50 a.m. EDT: Struck last couple of sentences and added update explaining why.
- 7-May-2008, 7:10 p.m. EDT: Edited away some small embarrassments — repeated use of “points out” in first para, mispelling of dealers, plural “spreads” where singular “spread” works better…

Steve:
Spreads for the dealing size you are looking at, are meaningless. Consider this, if you exchange $100 for euros at the airport, what is the spread ? And what is it for exchanging x millions of $ at JPMorgan. A lot lower. It’s no different for stocks or bonds, but you don’t know that because you are looking only at the “bureau de change” for stocks and bonds
May 7th, 2008 at 4:12 am PDT
link
Re jck’s comment:
The retail pricing of different financial assets reflects infrastructure and cost relationships between the professional wholesale market and a corresponding retail distribution network for that particular market. Within an integrated wholesale/retail bank, the typical distribution network for foreign exchange is fairly costly in terms of infrastructure and labour. Transaction costs are high. The spread for Euros at the airport is wider, but not entirely due to liquidity risk. Additional distribution costs must be absorbed by the spread.
Having said that, the distributor would be protected by wholesale market movements according to an intra-day transfer price set by the supplier (i.e. the trader). The duration and the frequency of intra-day resets on such transfer prices may change in volatile markets. But it is not necessarily continuous (particularly in banks with branch networks), and therefore it is fixed for some intra-day period. The rules are that the retailer’s margins are hedged for that period, and the supplier is exposed to the risks of the market relative to that fixed contract. This sort of price risk protection does not exist for equities and I suspect bonds are somewhere in between.
The typical distribution network for foreign exchange is somewhat unique and lowly in this regard. Within integrated banks, the gross margins are high, due to the usual infrastructure and labour costs of retail distribution networks. Contrast that with the distribution system and real time pricing interface for retail equities, and it is clear that the equity market has a much more highly evolved continuity between wholesale and retail pricing. Again, I suspect bonds are somewhere in between. Of course, it also makes a difference as to whether retail commission costs are captured explicitly as charged in equities, or implicitly as charged for bonds and foreign exchange. But still, the retail customer is insured against more intra-day wholesale price risk in the case of foreign exchange and bonds than is the case for equities.
May 7th, 2008 at 8:31 am PDT
link
jck — Of course you’re right that I am looking at quoted spreads on retail markets. I don’t pretend that’s the best measure — even retail investors often trade inside quoted spreads. It’s just the measure readily at hand.
But I don’t think it makes a huge difference. Yes, the spread one pays at an airport exchange booth is (very) retail, and much higher than you would pay in formal FX markets, or for large purchases private deals. But your comment implies that volume discounts would be the norm, for those who escape retail. That’s only right up to a point. An exchange booth has high fixed costs, and as JKH points out, somewhat hedged risk. In fact one can negotiate volume discounts at retail exchange booths, as one would expect given fixed costs and certain unit profits. If an exchange booth is fully hedged, one would expect the spread per dollar transacted to diminish monotonically, until rationing by cash-on-hand kicks in.
The FX desk at JPM might also give volume discounts, but not indefinitely. First off, they pay lower transaction fees than retail booth operators, so their minimum spread is less. They also have fixed costs of various sort, and an interest in retaining relationships with larger customers, so they give good price, special for you. I’m sure they’d be glad to do so for tens or hundreds of millions of dollars in the FX world. (Even retail investors can trade millions of dollars of FX at will and without triggering adverse price movements. At my broker, current depth at best-bid-and-ask on USD/EUR is $5 million each way, at a half-spread of 0.325 basis points. The quotes depth is ~$30 million both ways, but I the hald spread would increase by roughly 1.5 times if I pushed out that far.)
FX is the ultimate “paradoxical liquidity” market — nonspeculative liquidity traders are so predominant relative to informed speculators that dealers can offer very tight spreads and trade very large sums with little fear getting caught out by adverse movements before they can liquidate. But even in FX markets, eventually the effective spread you’d pay to do a deal would spike upward, and the rate at which different currency pairs would spike would be a measure of valuation uncertainty.
JKH’s point about specific hedging arrangements between retail and wholesale is interesting. I’m sure the bond spread I quoted above is very, very retail, and that even retail investors could do much tighter deals on small quantities just by putting limit orders in the spread. But as the volume of trade increases, the details become less relevant. A partially hedged bond dealer might expand her spread only slowly, because she is hedged and can offload much of the risk. But somebody is still bearing inventory risk. As deal sizes grow, eventually fixed commitments will be overwhelmed, and bearing risk will become discretionary, and priced.
If you are looking for a measure of valuation uncertainty (which is really what I was after in this disorganized mess of a piece), what goes on at small volumes tells you next to nothing. The shape of the curve as volumes get large, relative to the curves of other assets, that really tells the tale. At low volumes, “paradoxical liquidity” can be arranged — for good or for ill, many traders will read small volume spreads as informative, and take comfort in that.
But at the volumes where liquidity traders play, tight spreads just mean there are lots of liquidity traders. If you want valuation informative spreads, you have to look at spreads when “liquidity has dried up”, or out along the volume curve where those who accept a position can’t assume that liquidity traders will let them unwind it “at market”.
May 7th, 2008 at 1:40 pm PDT
link
steve:
I see your point. Spreads are a function of time in force among others things, so a raw spread itself gives you no information, for ex 1 cent for KO is a very expensive spread if good for 60 milliseconds and in comparison, your bond spread might be cheap if good for a week.
I don’t see how an illiquid market spread would give you more information, the spread would just be much wider and by an amount that’s a straight function of time.
May 7th, 2008 at 2:22 pm PDT
link
jck — re time, that’s certainly true. from the perspective of writers of the spread, as time goes to zero so too does risk, and so drawing inferences based on marketmaker willingness to bear risk gets questionable. here are two thoughts on the matter:
1) if it’s possible to have a measure of valuation uncertainty without a “by whom” caveat, that is a market-measure of uncertainty, then we’re not really interested in the duration of offerings that make up the spread, but in the spreads investors are likely to face if they choose to transact. If there are consistent offers at a 20bps half-spread, but 33% of the time there are transient inside limit orders (potentially each by different parties) such that at any point in time, there’s a 1 in 3 chance of only paying 10 bps, we’d want our measure to reflect our weighted average. We might construct a measure by choosing a depth and a period of time (say a day), define spread@depth as a function of time within that period, integrate and divide by t. We’d get a scalar. Compute at different depths, and we’d have a spread curve of the sort shown. That’d be fine, even if the value computed in large part was a function of very transient limit orders. It is the cumulative impact, of those orders, rather than individual risks taken, than interest us.
2) All that said, quoted spreads are impractical measures, quite because writing free options is costly, and the benefit that offsets that cost (capturing liquidity trades) is only available near the midpoint. The supply/demand schedule implied by a limit order book becomes increasingly censored as we deviate from the midpoint, that is at the higher depths where I claim they would be informative. I think effective or realized spread measures would be better, that compare (transaction price, volume) pairs to quoted midpoints at or before the trade to try capture hidden willingness to transact. So long as there is trading volume, we should be able to construct such measures.
(For markets that are entirely locked up with wide, quoted spreads, life is harder, although I still think that ones best estimate of valuation uncertainty is a function of the quoted spreads, but it might also be a function of other, e.g. structural, issues. Perhaps those who can best value the securities and those who post limit orders where they show up on Bloomberg are different groups, and in a real world with frictions, there’s no guarantee that they’ll get together and come to a mutually beneficial information-sharing arrangement.)
May 7th, 2008 at 4:19 pm PDT
link