The convenience yield
If a commodity is in “backwardization”, that is, if futures prices are lower than current prices, does that imply that futures markets are discouraging storage (encouraging disgorgement)? Paul Krugman makes the case, here and here.
I’m going to challenge him with a low-down, dastardly kind of argument. The gentleman keeps asking for evidence, evidence, and in response I’m going to offer an unfalsifiable hypothesis. Krugman says that futures prices are too low to cause people to withhold physical oil and sell forward, as required to affect spot prices. But whatever forward price curve he shows me, I can posit an invisible “convenience yield” large enough to make hoarding oil worthwhile. I don’t even have to be unreasonable about it. Extrapolating from historical data, we see that gently “backwardized” futures prices might be quite sufficient to encourage storage when convenience yields are taken into account.
Despite all of this, I agree with Krugman that futures markets can’t explain the recent skyrocketing oil prices. Not unusually, he’s been a voice of sanity and reason. But just as speculation in futures need not affect spot prices (if it is balanced long and short), speculative withdrawal of physical supply need not affect the shape of the future price curve. Futures market “signatures” can’t be relied upon to distinguish speculative from fundamental demand, and inventory may be unmeasurable, especially if it is offshore or takes the form of withheld production. Further, both futures in contango and measured inventory build can signify known fundamental demand as well as speculation. (Suppose entrepreneurs are planning to fire up many new factories over the next few months. If they buy forward to hedge their exposure to energy prices, that would push futures into contango and promote storage with no one speculating on anything.)
But this isn’t about that. This is a disquisition, and ode, a homage and a tribute to the marvelous, mysterious, misunderstood and maligned convenience yield:
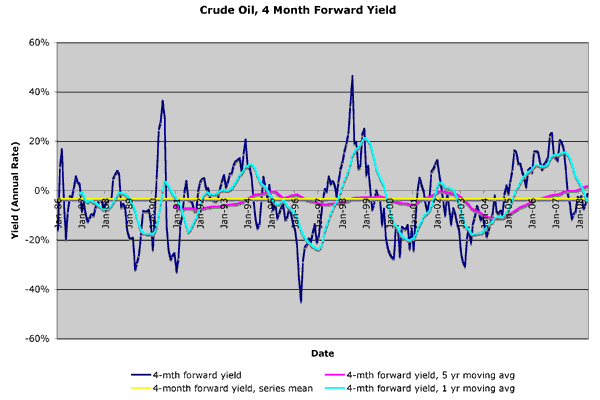
The bedrock principle of futures markets is “no arbitrage”, that is prices should be set such that there is no investment strategy that yields a risk-free profit higher than the risk-free rate of interest. For a physical commodity, this seems to imply that the forward price should equal the present price plus the risk-free rate of interest and any storage costs. Interest rates are never negative, and storing stuff always costs something, so you’d expect future prices of storable commodities to always be higher than current (“spot”) prices. But check out the following graph of the four month “forward yield” of crude oil. (Data courtesy of the EIA, hat tip Krugman, calculations and errors are mine, click for a bigger version).
The “forward yield” is just the percentage by which the future price is higher than the spot price. I’m using four month futures, but I’ve converted the yield an annual rate. If the forward yield is 10% and the interest rate is 4%, an oil man would profit from buying oil now and selling it forward, as long as his storage costs are less than 6% per year. Tycoons would start buying spot and selling forward until yield dropped to interest + storage.
But didn’t we say future prices should be higher than spot prices? Look at the average (the yellow line in the graph). It at -3.4%, well below zero! The yield is negative more often than it is positive. Whenever the yield is anything less than interest + storage, you’d expect oilmen to sell crude from storage and buy it back forward. He earns interest on his cash and saves the storage costs that way, which is better than the profit he’d make storing and selling forward. When the forward yield is negative, Texans should be selling physical and buying forward like mad. By doing so, they earn interest on cash, save storage costs, and lock-in an easy profit buying back their oil for less than than what they sold it for. Very quickly, all the selling should create a glut of physical oil, driving down spot prices, while the buying forward drives up future prices, until the yield is positive and sanity is restored. But negative forward yields for oil have persisted, sometimes for years at a time! We must be missing something. Hmmm…
Suppose someone offered to buy your vacuum cleaner today for $100, and sell it back to you next week for $80, with no risk of wear or breakage. Would you? It would depend how much you value the use of your snorter. If you refuse, we might infer that a week’s access to the pleasures of vacuuming is worth 20 bucks to you. We call that value of temporary use a “convenience yield”. It’s as if having the vacuum cleaner around pays you $20, even if no cash changes hands. Maybe we observe negative forward yields on oil because the smell of oil in the morning is priceless to guys in cowboy hats. (Or not… see below for a more plausible account of oil’s “convenience yield”.)
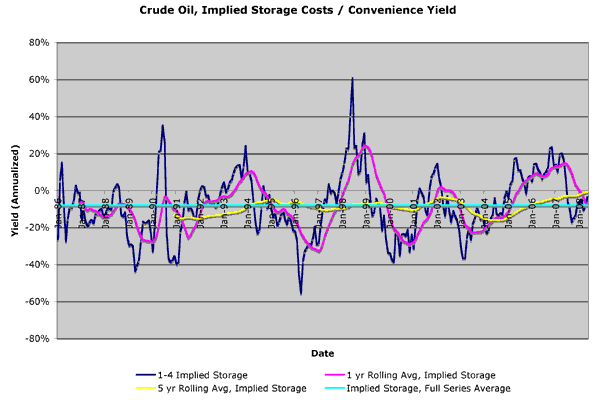
Let’s eliminate wandering interest rates, and take a look at the storage cost / convenience yield of oil historically. Below is a graph of a three-month forward yield (calculated from the first to the fourth month forward, because futures prices are more trustworthy than spot) with the concurrent 3-month T-bill rate backed out of it, leaving only storage costs. When storage costs are negative, that reflects, by definition, a convenience yield. (Again EIA monthly data, T-bill rates courtesy of FRED, my calculations)
From Jan 1986 through May 2008, oil futures have reflected a convenience yield of 8% per year on average. (This is in rough agreement with the overall mean of 0.021% per day calculated here by Milonas and Henker, see Table 3.)
Suppose that the current convenience yield is about 8% and three month interest rates are about 2%. Then a one-year futures contract should be about 6% cheaper than spot, and a four-month-out contract should be about 1.4% cheaper than a one-month-out contract (reflecting 3 months of storage). At the end of May, the 4-month-out contract was in “backwardation”, but was only 0.5% cheaper than the 1-month, still too expensive given the convenience yield. Oil dudes could have earned (on an annualized basis) about 3.6% more than the risk free rate (about 5.6% overall) buying high and selling low, but enjoying the privilege of storage. Now that oil is in gentle contango (as of June 17, the 4 month contract costs about 1% more than the 1 month), buying forward and storing looks like a really fantastic deal.
What is this “convenience yield”? Is it real? It seems like it must be, the economics of an 8% return aren’t subtle in the data. But when I first encountered this idea, it baffled me. So instead of talking oil, let’s talk hotels.
Suppose you have a hotel, it’s morning, and you’ve got a room that isn’t yet booked for tonight. Empty rooms end up costing you about $10 a night, considering your rent, maintenance, utilities, etc. But, you estimate there’s about a 50% chance that a weary last-minute traveler will come by and pay your walk-in rate of $150 for the room. So, the risk-neutral expected value of your empty room is $65 [(150 ÷ 2) – 10]. You’re risk-averse, not risk neutral, though. You’d accept a certain $60 rather than a 50-50 chance of losing $10 or earning $140. That $60 is the “convenience yield” on your empty room, it’s what having a room empty, in case opportunity strikes, is worth to you.
Oil is a “spiky” commodity. Every once in a while, someone really needs it, now, and will pay a premium for immediacy. The market for oil in Cushing, Oklahoma might be reasonably efficient, but what happens when someone in Peoria needs oil today? Opportunity! Instead of running a hotel, you build an oil tank in Peoria. Suppose that every month, there’s a 10% chance a desperate client will offer a 5% premium for immediate delivery of all your oil, and that interest and storage cost you 0.2% per month. Then on average, you’d earn 0.5% (10% x 5%) each month from desperate clients, and pay 0.2% in expenses. You don’t want to bear the risk of fluctuating oil prices, so you sell your oil forward. If you were risk neutral, you’d be willing to sell it for a discount of up to 0.3% less than you bought it for at the beginning of the month, at which price you’d just break even. But you’re not risk-neutral: You attach a “certainty-equivalent” value of only 0.4% to the unpredictable income from needy customers, and would offer no more than a 0.2% discount on month-forward oil sales. In the end, you earn a risk-adjusted 0.4% per month “convenience yield” from desperate polluters, and pay 0.2% in interest and expenses, and 0.2% in hedging costs. If one-month oil futures pay more than 0.2%-less-than-spot, or (golden days!) if they are in contango, you’d buy as much oil as you could and sell it all forward, because every new barrel that you promise to buy high and sell not-so-low represents certain (well, “certainty equivalent”) profit.
Putting aside Peoria and our artificial needy customer, sometimes oil spikes even on the wider market, so that anybody with physical oil can sell at a high price and while locking in low-priced near future purchases to replenish their stock quickly enough to meet any other contractual obligation to sell. If you estimate the profit you’d to earn from these occasional opportunities, and subtract a bit to come up with a “certainty-equivalent” value for this uncertain income stream, you’ll have determined a convenience yield. It shouldn’t be surprising that convenience yields are especially high for volatile commodities subject to frequent shortages and price spikes.
When futures markets are well-arbitraged (which might not always be the case!), the future price of a storable commodity is determined by the spot price plus the total cost of storage, defined as foregone interest, plus storage costs, minus any benefit of temporary ownership &mdash the convenience yield! When a storable commodity like oil is in backwardation, that doesn’t mean that the markets are predicting that its price will fall. It means there is a convenience yield. And in order to decide whether futures markets are creating incentives to store or to sell physical stuff, you have to estimate the convenience yield.
Postscript: While I was writing…
Mark Thoma offers a nice extension of Krugman’s model, showing how monetary policy, by affecting interest rates, would be expected to affect storage.
Yves Smith offers very pointed commentary on futures markets, speculation, and inventory (here and here).
If policymakers want to “do something” about commodity speculation, they should really start investigating passivity on the short side of the market rather than enthusiasm on the long. Given what’s before them, I hope they ignore Michael Masters (ugh!) and Thomas Palley (whom I often like, but yuk), and go with Dean Baker’s suggestion of a Tobin Tax (ht Mark Thoma).

It is interesting that even if officially Oil producers are trying to extract and sell as much Oil as they can the futures market could create huge incentives for them to hoard and not extract.
June 25th, 2008 at 7:26 am PDT
link
Steve,
You have shown that the futures price can affect spot even if it is below the spot price. Your argument is, as you say, unfalsifiable. However, if the forward curve is in backwardation (large convenience yield) that would suggest that inventories are low (or lower than desired levels). If the futures and spot prices have increased so much and inventories are still low, physical supply and demand must be in balance. Haven’t you just proved Krugman’s point?
June 25th, 2008 at 8:20 am PDT
link
Haven’t thought this through, but it seems like the convenience yield should be relatable somehow to the value of an at the money call option on oil.
June 25th, 2008 at 8:37 am PDT
link
Suppose someone offered to buy your vacuum cleaner today for $100, and sell it back to you next week for $80, with no risk of wear or breakage.
And suppose it costs you $40 to find your vacuum cleaner and get it out of the
groundcloset…June 25th, 2008 at 8:49 am PDT
link
All very interesting except that the crude oil futures contract is priced for oil “in flux” [pipeline], not in storage. So your carry calculation should include the costs of taking delivery [removing oil from the pipeline], storing it and for re-delivery cost of finding a spot in the pipeline…etc.
The producers have oil “in storage” [in the ground]. Backwardation means better sell now for spot than for future delivery, contango the reverse, leave it in the ground and deliver later.
June 25th, 2008 at 11:29 am PDT
link
Came across this separately today:
“Economists explain backwardation using the term “convenience yield,” which is something of a fudge factor. People don’t sell their stocks of a commodity when there is backwardation, hence they must get some utility from holding the stock, so let’s call this “convenience yield.”
Perhaps a more plausible story would be option value. If you retain your oil even when there is backwardation, you have the option of selling it later. On average, it looks like you will forego profits by selling it later, but with volatile prices there is the chance that you will get to sell it at a much higher price. If you sell the oil now, you do not have such an option. When oil prices are volatile, the option value is high, so you keep your stock of oil even if the futures price is below the spot price. For this story to work, there has to be an asymmetry in possible oil prices. That is, you have to believe that there is a floor, but not a ceiling. I suspect that the floor has to be rather high in order to matter–zero probably will not do.
In short, my model of the oil market is this:
1. Speculators determine “the” price of oil by placing bets in the futures markets that reflect expectations for the entire future path of demand, discovery of new oil reserves, development of alternative energy, etc. There is no such thing as a “signature” for when future-oriented speculation is determining the price. Future-oriented speculation always determines the price–high, low, or in between.
2. The relationship between spot and futures prices should be based on the Hotelling principle, which would imply that futures prices would be above spot prices, with the differential approximating the rate of interest. If the spot price were too low relative the futures price, producers would extract little oil, if any. If the spot price were too high relative to the futures price, producers would use up their oil too quickly.
3. If there is a floor on oil prices without a ceiling, then keeping oil in the ground potentially has option value. With volatile oil prices, there is an additional incentive to leave oil in the ground. For a given level of futures prices, the option value causes spot prices to be higher than what the Hotelling principle would predict.”
http://econlog.econlib.org/archives/
2008/06/my_model_of_the.html
June 25th, 2008 at 4:11 pm PDT
link
anon — I think your intuition about convenience yields and option value is right on. Scanning briefly the academic abstract on convenience yields, there’s a lot borrowed from options modeling ideas, and analogies are made to call options. (I like the model in this paper, which is very straightforward, although seems to presume perfect ability to time transactions. — Approximation for convenience yield in commodity futures pricing, Heaney.)
Kling’s discussion (which I mostly like) is a bit murky on exactly what kind of option a convenience yield represents. The important to thing to remember is that a convenience yield represents not an option on the price of a good, but the option on a fixed-period calendar spread. Convenience yields grow as the price differential between near-term and further-out prices becomes more volatile. A “parallel” shift in the price of a commodity, that is a broad rise in the price of oil over all time horizons, does the convenience-yield arbitrageur no good. Our yeoman hoarder will have purchased physical stuff and committed to selling it forward for less than what he paid. If the price of the stuff rises, he still has sell at the precommitted price. He can sell transiently and but he must commit to repurchase prior to his commitment (or gamble), and if his repurchase price is as high in time-value adjusted terms as his sales price he gains nothing.
However, if the shape of the period forward price curve is volatile, that is, if the price might rise in the near future while falling or rising more sluggishly at a period further along (but no later than the precommitted sales date) , the out hoarder profits, and that possibility is the source of the convenience yield.
The paper linked above takes a very simple view. It view the convenience yield as the spread between the maximum spot price over the fixed period of ownership and the price at the end of the period (when our hoarder will have meet his commitment by repurchase or offsetting his commitment). If that spread is large and positive, kaching, if not the trader has no cashflows. You can see how optionlike that is: the cost of the strategy is predetermined by the level of backwardation (fixed premium), worst case scenario is zero cashflow at maturity, “in the money” scenario is positive spread between an intermediate price and the price of the good at end of period. (I’m not sure whether the paper takes the end-of-period price to be a price contracted at the time of sale, or whether the trader takes on price risk by waiting to end of period. If the latter, it’s no longer so option-like… I bet he means a precommitted price, but I’d have to go back and look.)
More realistic approaches would include the possibility that commodity owners might sell and repurchase prior to end of period, and engage in multiple such transactions. (For convenience, one might just try to value very short period, one-transaction options as above, and consider a long period a portfolio of sequential options.) Also, one would need to model the uncertainty traders face in the optimal timing of trades. When a spread is positive, is it better to wait for it to widen yet more, or pounce on a good deal? One would have to pair modeling the price behavior with some optimal timing strategy to estimate value.
Anyway, it’s an interesting phenomenon, and more general than people think. I don’t like referring to convenience yields as a “fudge factor”, although that’s common, because it clearly represents a real economic asset, even if we can value it only imperfectly. There is nothing new about the idea that asset values are often and uncertain and require markets for price discovery. The chart in the post shows market pricing of the convenience yield as sure as a stock chart shows how much a firm costs.
Interestingly, stocks can be said to have convenience yields as well as commodities. And interest rates themselves are convenience yields that accrue to holders of cash. (Think of short-term interest as little repos. You sell the cash, and for a guarantee and can buy the cash back and a bit more when you surrender the guarantee in a precommitted roundtrip.)
Anyway, blah. Excellent intuition, though, on the option-like nature of convenience yields.
June 25th, 2008 at 5:16 pm PDT
link
Fullcarry — Here’s a paper that goes so far as to suggest that without backwardation, production would not occur at all! That is, even with a flat futures curve, the incentive to produce is much diminished. Backwardation in Oil Futures Markets – Litzenberger and Nir Rabinowitz
anon — The paper cited above points out that oil reserves are like options in the sense that Kling seems to describe. As oil price uncertainty increases, so does the option value of reserves, and the incentive to withhold rather than to produce increases.
June 25th, 2008 at 5:37 pm PDT
link
MG — I think that the relationship between backwardation and inventories is more complicated than you think. Remember, convenience yield is large when the price curve is volatile, not just prices themselves. It’s certainly true that one way for this to happen would be for inventories to be low in some places but not everywhere: then outtages would create local price spikes, but near future prices would remain low. But if inventories are low overall, then prices are likely to rise broadly. You’d not see spikes one day and cheap oil the next, as widespread shortages would drive up demand for whoever still has inventory.
At “normal” levels of inventory, the oil convenience yield seems to have been roughly 8%, which is way more than enough to put us in serious backwardation (goven 2% interest rates and small storage costs). That is, the existence of backwardation doesn’t really support a contention of low inventories, although some low inventory patterns might exaggerate backwardation. Backwardation can be high even when inventories are high, as long as shape of the forward curve is volatile. It’s possible, but by no means certain, that high “buffer stock” inventories would diminish this shape volatility. That’s a question that would take a lot of headscratching and evidence to make sense of, at least for me. (After all, inventories are small relative to long-term supply and demand, and the price of goods in inventory are forward-looking, not determined by the cost at which the inventory was acquired.)
June 25th, 2008 at 5:49 pm PDT
link
jck — re incentives and backwardization/contango, I agree directionally, but don’t think there’s anything special about the zero point. That is, increased backwardization encourages production, and increased contango encourages storage, but a 1% backwardization might not be sufficient to make production worthwhile.
You’re right to point out that the “convenience yield” faced by producers is less than that faced by those with above ground storage, because producers are technically constrained in terms of how they can time their commitments (and have limited capacity to repurchase and store as in the canonical convenience yield trade). That producers face technical constraints on the timing of flow changes, though, doesn’t mean a complete absence of discretion short or long-term in timing their production.
My guess is that producers view themselves as earning very little “convenience yield” that would justify accepting below spot future sales commitment. Their participation on the short-side of the futures markets would have to be driven by a string desire to hedge price risk (or speculating that prices will fall), since they have a lower benefit of carry than other players. As above, they profit from the option value of uncommitted reserves, so in times of high (but symmetric) volatility and no near-term liquidity/distress issues, producers would probably prefer to maximize option value by holding reserves uncommitted in the ground than to hedge risk by selling forward. Which might explain some of what we’re seeing. Without speculating on the direction of price moves, producers have the most incentive to produce when futures are in deep backwardization due to convenience yield they can’t earn while the overall price level is relatively stable. That would imply volatility in the shape of the forward price curve but not its overall level.
June 25th, 2008 at 6:02 pm PDT
link
Nemo — That’s a good point I never thought of (apropos the previous comment). Producers might enjoy a convenience yield that other parties don’t. If extraction costs rise more slowly than their real interest rate, they enjoy a convenience yield defined by the benefit of deferring production.
June 25th, 2008 at 6:05 pm PDT
link
“Interest rates are never negative . . .”
that’s true for nominal rates. does inflation adjustment of interest rates make any differance in your calculations?
June 25th, 2008 at 6:05 pm PDT
link
bob — Not from the perspective of the arbitrage argument. For a commodity with no convenience yield, if forward prices are not nominal interest + storage, you can make a certain dollar profit on no net investment (you can borrow money, earn more than the nominal interest rate with zero risk, then pay it back). So however quickly the dollar is depreciating in real terms (as long its its value doesn’t go to zero), it is still profitable to perform the arbitrage as much as you can, until prices correct.
June 25th, 2008 at 7:03 pm PDT
link
Krugman comes very close to assuming what he seeks to prove with his assumption about expectations and price, it seems to me. Why couldn’t the relationship between current price and expected price change be positive? Didn’t convince me.
I found your explication, Steve, of convenience yield instructive (I don’t do futures). You mention uncertainty (volatility). Isn’t it possible that market participants place a huge premium on certainty (having the oil they need today–today) above and beyond interest rate, and hence while paying high prices in uncertain times in the spot market are less willing to throw good money after bad in the futures markets–in long or short positions? This would imply a budget constraint on oil-related investments or expenditures.
June 25th, 2008 at 9:34 pm PDT
link
Having suggested the option intuition, I’m struggling to make full sense of it, being no expert on options on spreads.
Assume an idealized model where interest and storage costs are 0. This backs out the convenience yield more cleanly. Suppose both spot and futures would trade at $ 135 in a perfect arbitrage world.
If actual spot is $ 140 and actual futures are $ 130, the convenience yield is $ 10.
My interpretation is that $ 10 in this example represents the spread that traders are willing to pay for the “convenience” of holding spot oil, given the perceived volatility in the spot/futures spread and potential for it to widen further. If spot/futures arbitrage were perfectly continuous, then spot and futures volatility would move in tandem and the spread would have no volatility and no option value. Indeed, it would become 0. In reality, periodic spot volatility outliers and asynchronous spot/futures volatility patterns overwhelm any possibility for spot/futures arbitrage to be perfectly continuous, so there is volatility and risk in this spread that becomes exploitable by traders.
If this interpretation is correct, it seems like a self-referencing construct in terms of option content, and I have difficulty distinguishing between the underlying and the option in this case (both spreads?).
The other question I have is (having stripped out interest and storage costs for presentation purposes) why the spread should necessarily be skewed to the call option direction, if direction is defined as spot minus futures. It implies I think that the spot market has greater volatility than the futures market, which seems intuitively correct, given the description of the physical examples. This combined with asynchronous volatilities gives the option value its “juice”.
June 26th, 2008 at 12:12 am PDT
link
Benign — It sounds like your suggesting a loss of confidence in futures markets, that those who know they will require the physical commodity prefer to bear all the costs of holding it because they fear futures contracts wouldn’t be honored. If only “longs” were afraid of nonperformance, I guess that would show up as a convenience yield, a discount in the future prices to compensate people for their fear of nonperformance. But if there was a widespread fear of a breakdown, would shorts who intend to sell a commodity also be concerned that delivery won’t be taken as agreed? You could argue that there’s an asymmetry — a long generally has storage as an option, while a short may intend to sell a commodity she has not yet produced, so the option of selling now, buying certainty by offering a spot discount, is not really an option.
Why would that imply a budget constraint, though?
BTW, in the scenario I’ve described (which I’m not sure is the one you meant to suggest), there’d after be uncertainty that contracts would be fulfilled. Mere volatility of prices would not discourage people from using futures markets, because prices are locked-in.
(Well, that’s not quite true. People are exposed to the risk of being required to post cash margins if there are large price fluctuations, even if they are short and have plenty of commodity to sell. So price volatility can discourage liquidity constrained actors from participating in futures markets. Is this what you mean by a budget constraint, that limited budgets combined with price uncertainty wouldforce people from futures market for fear of liquidations forced by margin requirements?)
June 26th, 2008 at 1:58 am PDT
link
anon — I think your interpretation is correct. The underlying is the spread between a near-term future price and any longer-term future price prior to the main contract’s expiration. When you enter into the “main contract” to sell your physical stuff forward, presumably the market was in a “no arbitrage” equilibrium, implying there was not some buyer willing to buy at a higher price than you’d pay to recover the stuff. The spread between what you’d earn in a quick sale and what you’d pay to buy the commodity back, including your savings in interest and storage, would be zero. But, suppose s— happens, and there is a temporary shortage, so you can sell and repurchase your stuff for a profit. Then the spread between your near-future sell price and further-ahead repurchase price + saved interest and storage would be a positive number. This spread, this number, is your underlying.
The option is your capacity to enter the trade. Mere ownership of the commodity would have conferred this “real option”, but the fact that you have retained this option while selling it forward means you get the benefit when a favorable spread emerges, but bear no risk of unfavorable price changes (whether temporary or long lasting). The premium you pay (in the discounted forward sale price) puts insulates you from exposure to all adverse price moves, while you retain exposure to some favorable price moves, exactly like an “at the money” option.
Whether you call it call-like or put-like strikes me as ultimately semantic. The exercise price is zero, so it doesn’t matter whether you pay or get paid X. The spread can move in a favorable direction or an unfavorable direction (suppose near-future prices fall due to some glut on the market while further future prices stay constant), but you simply don’t transact on unfavorable spreads, just like you wouldn’t exercise a call option when a stocks price is less than the exercise price, or just like you wouldn’t exercise a put option when the strike price was above. Ultimately, when you are long any option, you get paid when relative prices move in some direction, while you lose nothing (other than the initially paid premium) when relative prices move in some other direction. With ordinary calls and puts, one of the two prices is fixed. Here both move.
Payoffs after exercise:
Call = max[S-X, 0]
Put = max[X-S,0]
Convenience Yield = max[(e^(r Δt) CP1)-CP2, 0]
…with CP1 = a near-term commodity price and CP2 = a longer-term commodity price (but no further out than the close of the “main” futures contract) and the e^(r Δt) factor accounting for the interest you earn on your temporary cash position. (Note that exercise of an ordinary put or call is instantaneous, but exercise of the convenience yield option is not. I’ve put the “after exercise” value.)
Ignoring the interest factor (which will be very close to one if it’s a very transient spike you are exploiting) the payoffs are just…
Call = max[S-X, 0]
Put = max[X-S,0]
Convenience Yield = max[CP1-CP2, 0]
You can say that the CY is “call-like” by calling CP2 the floating “exercise price” or “putlike” by thinking of CP1 as the exercise price. It doesn’t really matter, and you needn’t think of it either way, just let it be its own thing.
(p.s. I edited this slightly after posting… I realized I’d messed up a bit of the math.)
June 26th, 2008 at 2:45 am PDT
link
All — I’ve been reading the paper cited above that argues that oil-in-the-ground can be modeled as a call option (whose exercise price would be extraction costs), which idea served as the basis for some speculations above. I’m less sure than I was that it’s a good way of thinking about reserves. So, please scratch some of the conjecture based on that. Also, I misspoke when I said that according to the paper, producers would only produce in backwardation. They have a concept of “weak backwardation”, meaning forward prices less than spot+interest+storage, but not necessarily less than spot in absolute terms. In their model, producers will only produce if futures prices are backwardization or “weak backwardation”.
None of this affects the conversation about convenience yields, a large part of which can straightforwardly be modeled as an option.
June 26th, 2008 at 2:57 am PDT
link
Steve, time and again your posts and comments are one of the most valuable resources on the internet.
I think there is a fundamental methodology problem with Krugman analysis and most of the related public discussion as all analyses I’ve seen are based on near-equilibrium models. You are not going to ‘see’ a bubble in near-equilibrium models the same way you are not going to ‘see’ an explosion in near-equilibrium thermodynamics. The very essence of explosions (and bubbles) is that they are dynamic phenomena that can only happen far from equilibrium.
For bubbles to happen for example you need a reservoir of greater fools that flock into the bubble asset in growing numbers until the bubble burst. Any model that doesn’t include ‘greater fools’ and time will never ‘see’ a bubble. Ask the NAR.
June 26th, 2008 at 3:08 am PDT
link
Steve, one more point I don’t like about Krugman analysis is that he uses a classic price-demand curve for oil. As long as portfolio investors (aka speculators, aka greater fools) buy future contracts they are actual demand. The price-demand curve for them might very well be inverted (higher price stimulate higher demand) and if their number grow with time the total demand of future oil will change with time pushing the future price higher.
Then arbitraging will move the higher future prices to higher spot prices as you explained. I guess (but I will trust your opinion better) without any need of physical inventory.
June 26th, 2008 at 3:17 am PDT
link
Steve: Thanks for the respone.
I think representaion of the value of inventory as an option on the spot-future spread is on the mark. However, I believe that spread volatility will be inversely correlated with inventory levels. Low inventories will increase the volatility of spot prices, and futures are inherently less volatile than spot because they allow time for markets to adjust by shifting supplies or adjusting production schedules. So backwardation will tend to be associated with low stocks.
June 26th, 2008 at 7:58 pm PDT
link
Steve, yes, great blog!
Knightian (not “volatility”) uncertainty could cause both a very high convenience yield and fear of failure of the futures markets and reluctance to throw “good money after bad.” Margin requirements would eat into liquidity (it was late when I said budget constraint).
I don’t think the regulators are going to solve the problem of high spot market prices. Further doubts about execution in the futures markets might only drive spot price higher. My tired brain’s final take on this is that it doesn’t matter whether you call it speculation or financial high fashion when the big money piles in and bids up prices. The BP data suggests the price rise is due to a demand shift against relatively inelastic supply. [Whether speculators are making money manipulating spot vs. futures prices a la Jim Cramer on a very short-term basis is another question.]
June 26th, 2008 at 9:27 pm PDT
link
Options Intuition Redux:
A trader can put on a spot/futures hedge and protect downside risk while seeking net gains by trading the spread. E.g. If an initial $ 140/130 long spot/short futures position moves to $ 145/125, the trader can close out the initial position and realize a net gain of $ 10 on an original spot price of $ 140. The trader might have otherwise run an un-hedged long position and made a profit of $ 5, but has improved on this outcome by trading the spot/futures spread, which was more volatile than spot alone. And he was protected on the downside while waiting for the opportunity. It seems like a very good deal if it happens, and it doesn’t seem unreasonable that such an opportunity should occur given some decent volatility in the spread relationship. As per the discussion above, the opportunity to make such profits can be attributed to a “convenience yield” that equates to an option on the spread.
The question is why in an efficient market is it reasonable to expect that such opportunities and such “apparently” “free” options will exist for traders?
My interpretation is that traders bid up the market price for convenience yield because they have the opportunity to trade spot/future hedged positions rather than sit on them as fixed hedged positions. Traders seek to exploit the value of volatility and can be flexible in their strategy time horizons. Traditional non-trading hedgers seek hedged price stability and want fixed hedging time horizons. Price volatility and time uncertainty therefore offer option value for traders. Thus, convenience yield as a spread option is attractive to traders. As spot/futures spread pricing component, it represents the expected value of the trading profit possible by being long spot while being hedged with futures. And traditional non-trading hedgers also pay this convenience yield as a hedging cost component, which in fact has been created by traders in their pursuit of related spread volatility trading.
….
“Whether you call it call-like or put-like strikes me as ultimately semantic.”
My question was slightly different than this, so let me recast it.
In a “normal” commodities market, futures prices should exceed spot prices by an amount that is equivalent to interest costs and storage costs. Any deviation from this is explained by convenience yield. If the futures price curve is in backwardization, the difference from the implied contango curve is due to convenience yield.
Thus, convenience yield as a marginal spread pricing component makes the spread between spot and futures prices less negative or more positive, and the futures curve less contango’d or more backwardized.
This leads to modeling convenience yield as an option on a positive spread component between spot prices and future prices, or a call option on spot prices at a floating futures price strike, or a put option on futures prices at a floating spot price. In all three modeling constructs, the marginal effect is assumed to be a positive convenience yield effect in terms of the spread between spot and futures being made less negative or more positive. This adjusts the standard contango futures curve in the direction of marginal backwardization.
However, your first graph shows some significant volatility in the 4 month forward yield on oil over the past 20 years. Furthermore, the exhibited volatility is conceptually symmetric in a rough sense – it shows spikes in both backwardation (lower part) and in contango (upper part). The backwardation spikes would seem to represent great trading opportunities for realizing outsized convenience yield gains.
At the same time, the contango spikes would seem to represent some sort of similar option like volatility opportunity. These contango spikes seem to be well in excess of interest rate and storage costs (interest rates in some periods were high, but not that high). This would imply negative convenience yields as defined.
It seems logical to ask the question as to whether the convenience yield does become negative in some of these contango spikes. If so, what does it mean? Does it mean that traders should be entering these periods with short spot / long futures positions? Can traders attempt to take advantage of downward spikes in the price of spot oil and spot/futures spreads? And does the idea that they would not immediately close a negative convenience yield position with arbitrage profit again represent the price they are willing to pay for the opportunity of such downside volatility trading?
And so I think what I’m really asking is whether the subject of convenience yield includes the case in which traders can employ put strategies in (spot – futures) terms, and where convenience yield can become negative in markets where the volatility of (spot – futures) is skewed to the downside.
June 26th, 2008 at 10:51 pm PDT
link
anon: “It seems logical to ask the question as to whether the convenience yield does become negative in some of these contango spikes. If so, what does it mean?”
You could interpret it as a negative convenience yield or as an increase in the marginal cost of storage as conventional storage tanks fill. I think the latter is more appropriate as any option value in this case would be directed toward investment in incremental storage capacity.
June 27th, 2008 at 7:48 am PDT
link
MG:
Yes. That makes sense assuming there is observable confirmation that the increase in the observed contango is indeed the result of increased storage cost. And it makes sense intuitively when spot is falling and inventories are increasing.
But is the storage cost interpretation also meant to complement the idea that convenience yields must always be non-negative? Does the potential for negative convenience yields make sense in theory and practice – or is it meaningless and impractical? I don’t know.
June 27th, 2008 at 8:31 am PDT
link
anon: “But is the storage cost interpretation also meant to complement the idea that convenience yields must always be non-negative?”
The problem with negative convenience yield is that it implies that the foward price exceeds the spot prices by more than the cost of storage. This shouldn’t occur unless you are out of storage space. In this case the spread includes the shadow price on storage capacity and volatility in the spread would increase the profitability of adding capacity.
June 27th, 2008 at 8:43 am PDT
link
MG:
Thanks. Sounds too good not to be right.
I must go back to a textbook and review shadow prices :)
June 27th, 2008 at 8:48 am PDT
link
Hi Steve, I’ve been discussing this over at Economist’s view and finally checked out the comments here and I see that you guys have already covered of the thoughts I had re: convenience yields and options premiums in a lot more detail, but I came across an article that might be of interest:
The Information Content of the Implied Convenience Yield: Using American Call Option Based Structural Model
Abstract:
This study examines the relationship between volatility and the spread of two commodity futures with different maturities in the NYMEX crude oil market. We find that convenience yield behaves like an American call option, which suggests that the information content of convenience yield is volatility behavior. Our model successfully quantifies the sensitivity of the spread with respect to volatility and provides satisfactory predicting power. For practical applications, we show how to calibrate our model in a trading strategy that can generate significant profit. Our structural framework lays the groundwork for studies on how volatility dynamics are related to commodity fundamentals.
Chen, Te-Feng, Lin, Ming-In and Wang, Kehluh, “The Information Content of the Implied Convenience Yield: Using American Call Option Based Structural Model” (January 2007). Available at SSRN: http://ssrn.com/abstract=957621
June 28th, 2008 at 12:16 am PDT
link
Alessandro — Trust me… anything I know about “greater fools” comes from spending too much time with myself.
I agree with you, generally, about the hazards of using equilibrium and near-equilibrium models to describe a world that is always in disequilibrium. That said, my head is too small to make sense of the variety of ways the world can be out of kilter, so I do see the use in looking at equilibria that might obtain under some circumstances, sometimes because beneath all the chaos, equilibria might be the “attractors” that help us predict a broad direction, and sometimes just as a way of structuring a conversation about why simple equilibria do not hold. You just proved this point yourself: Krugman posited a relatively “normal” near-equilibrium model, and you objected, pointing out very specifically an assumption that might not hold (the monotonically decreasing demand curve). For the conversation, both conjectures were useful. For reality, deciding whether a model is “right enough” that we should consider it broadly descriptive, or “wrong enough” to become a way of explaining why one might expect won’t happen, is a judgement call.
Speculative demand for futures contract should indeed lead to arbitrage until the spot and futures curves are in balance, but that can happen in a variety of ways. Krugman is right to point out that spot markets must clear, one way or another, so that if “index speculators” were buying futures contracts and no other market participants were altering their behavior except to exploit arbitrage opportunities, there would have to be some form of inventory accumulation. It might not be measurable (probably lots of inventory in the world, both above and below ground, evades any inventory statistics you might find). One question is whether that’s a ceteris paribius too far. There are lots of moving parts in the oil market (as in many markets I suppose).
Your comments suggest a suspicion of a pure speculative euphoria, of momentum buying by ever greater fools. There could be a lot of that going on, but again there are a lot of different kinds of market participants. With a stock bubble, it’s easy to see why people who “know better” don’t go short in sufficient numbers to pop the thing: all shorts are unhedged, except for the firm itself. The firm can short itself by issuing more stock, but managers tend to prefer their stock remain overpriced, even though existing shareholders might be better served in the long run if they sold new equity at outrageous prices. With oil, a similar dynamic must hold, if there is a speculative bubble. Oil producers can sell into the futures market full hedged by their production capacity. They could make it quite hard for a bubble to inflate. But to the degree they can accommodate a bubble by not selling into outrageous prices, they can help it last a little bit longer, make it possible for the spec-frenzy dynamic you describe to take hold. They must believe they’ll do better by selling overpriced oil for as long as it lasts than they would be eating speculators lunch in a bear raid. That decision, whether to forego certain short-term arbitrage profits in favor of riskier “bubble price” profits that depends on how the bubble lasts is an interesting one to think about, and why (I know I’m a broken record on this) I think whatever will turn out to be interesting about the current run-up will have less to do with the speculators than the producers.
Why aren’t producers selling their entire expected production capacity forward at ~$140/bbl?
June 28th, 2008 at 6:53 pm PDT
link
MG — I don’t disagree with you. As you suggest, it seems natural that spread volatility would correlate to some degree with inventory levels, as local shortages would be more frequent when, on average, people were low than when everyone’s tanks are full.
But the correlation coefficient wouldn’t be one. An increase in convenience yield still could occur when inventories were not broadly low, if something else were to make the shape of the futures curve more variable. For example, the alleged “index speculators” very well may be frequently inflating the 2nd and 3rd month out contracts relative to further future contracts, enhancing the convenience yield for those with selling forward into longer-term contracts.
So, I agree that backwardation will tend to be associated with low stocks, but not uniquely or necessarily so. All else equal, low sticks ==> tastier spread volatility, but all else needn’t be equal.
June 28th, 2008 at 7:14 pm PDT
link
Benign — Do you think that what’s going on is that people are in fact buying physical, eschewing futures markets but not having their inventories counted by whoever counts inventories? Given your reasoning, this strikes me as the right thing to do. There’d be an opportunity: liquidity constrained producers would avoid selling forward very far for fear of margin calls they’d be unable to meet in uncertain futures markets. Longs who buy outright and unleveraged via futures don’t need to fear margin calls (they keep sufficient funds in the bank to meet any margin, synthesizing simple ownership), but they do have to worry about nonfulfillment if they really do think the markets might fail. So, the right play would be oil in a tank purchased from liquidity constrained producers who sell either for cash or forward with fixed collateral, if you think oil is a good bet. Do you think that this is what’s going on, old-fashioned buying of physical buy people we cannot see?
Note that within the futures markets themselves, the implied convenience yield seems to be decreasing, that is, the markets have moved from backwardization to flattish with a brief contango hump in the near-future contracts. So the “convenience yield” you are describing isn’t showing up in the markets, but then those who think the markets will fail (or fail them with margin spikes) wouldn’t necessarily have their views priced into the curve.
June 28th, 2008 at 7:25 pm PDT
link
“(I know I’m a broken record on this) I think whatever will turn out to be interesting about the current run-up will have less to do with the speculators than the producers.
Why aren’t producers selling their entire expected production capacity forward at ~$140/bbl?”
Steve, dollar depreciation is the engine that’s driving this oil train. This depreciation MUST continue for the simple fact that current and future liabilities far exceed(in real terms)the potential productive capacity of the US.
With this information known by producers, hedgers and specs AND the FED validating this with their refusal to raise irates to slow this depreciation, a SUPER BUBBLE can/wil be inflated. Producers do NOT have to worry about the bubble collapsing since the dollar depreciation guarantees the floor.
June 28th, 2008 at 9:26 pm PDT
link
anon — Nice summary:
I agree with MG on the “negative convenience yield”… it looks more like a storage cost. But I think the heart of your question is whether there should be some kind of symmetry: if those long spot, short forward can earn a convenience yield from high-frequency sell-repurchase transactions when the shape of the forward curve is volatile, shouldn’t there be someone who can earn a yield from the opposite trade, buy spot and sell forward on downspikes in the near-price of oil not matched in longer time? Of course there should be, but the “convenience yield” for this party is going to turn out to be terribly innocuous. Just flipping the trade, instead of buying oil on a near horizon and selling it far, we’ll sell oil on a near horizon and buy it far. (Imagine we are an oil tank half full, we could make either trade.) Then we have cash in hand to buy oil when a spread arises in the forward curve lets us make a high-frequency buy/sell.
We have to distinguish here between purely financial spread traders, and those who can actually take and resell the oil. The “convenience yield” on buy-near-contract/sell-further-contract spread trading opportunities is available to anyone with cash, so in a risk-neutral world the expected yield could be no more than the interest rate. It’s not a risk-neutral flow, and cashflows from transient spread opportunities are volatile, so investors should demand a risk premium. But an ETF that engaged in this strategy: hold cash, occasionally buy-near-future-oil/sell-far-future-oil should earn no more than the interest rate plus perhaps a bit of compensation for uncertainty in the timing of cash flows. In risk-adjusted terms, the convenience yield to financial traders for having cash-in-hand for transient opportunities must be the risk-free interest rate.
People with non-full oil-tanks have an advantage over purely financial traders, because they can exploit volatility in spot prices that might be damped even in near future contracts. As MG suggests, this is basically a convenience yield to storage, and this could significantly exceed interest rates, since storage (like the commodity) is scarce and unevenly distributed. Someone with an empty tank and no futures position would earn this convenience yield, but if they plan eventually to hold some oil, this yield is overwhelmed by the risk that prices will rise against them. If they buy forward, though, their price risk is hedged, but they still earn the convenience yield to storage. If this is large, they should be wiling to pay a bit more for the oil they are buying forward than they would if storage was plentiful. That is, they should be willing to bid oil futures into contango, since they are compensated by a convenience yield on periodic needs for storage.
It’s counterintuitive, but in expectation both trades earn a convenience yield, even though at any given time, one trade profits only when the other does not. A half-full oil tank that sells now and replenishes forward earns in expection positive money on spikes in storage costs, while the same tank if it buys now and sells forward earns a yield on spikes in the price of oil, when storage is plentiful. It’s exactly analogous to conventional options: you pay a premium for an at-the-money call option or a put option, even though both can never profit at the same time.
At equilibrium, half-full tanks should be indifferent to the two strategies. Setting the interest rate to zero for simplicity…
CY-on-storage – forward-yield = CY-on-oil + forward-yield
CY-on-storage – CY-on-oil = 2 * forward-yield
If the forward-yield is negative (backwardization)…
CY-on-oil > CY-on-storage
…and if positive…
CY-on-oil < CY-on-storage
When the two yields are identical, the forward yield should be zero (or the risk-free rate, if we put interest back into the picture).
(The interest isn’t a big deal… with interest, CY-on-oil becomes CY-on-oil-minus-interest-rate while CY-on-storage becomes CY-on-storage-plus-interest-rate, and the rest stays unchanged. The spread between the two yield becomes…
CY-on-storage – CY-on-oil = 2*(forward-yield – interest-rate)
I think that just the midpoint changes.)
So, if we observe a forward yield of 1%, and an interest rate of 3%, and if we think the world is at equilibrium, a half-full tank would in expectation earn some positive wealth by either strategy, but would earn 4% more as a convenience yield by holding oil and selling forward, but would lose the same 4% in foregone interest (2% on money tied up in oil purchased, 2% more in interest that could have been earned if the oil had been sold).
We know what the spread is between these two yields, but what will the yields be in absolute terms? We know they will be no less than zero, and they should both be a positive function of spread volatility. With a sufficiently turbulent yield curve, the expected return to spread-trading for those hoping to make high-frequency sell-and-repurchase trades might be 10%, while someone pursuing the opposite trade (high frequency buy-and-resell) would expect to earn 6%, plus an additional 4% in interest. (These yields would be earned on the capital that might be invested in oil to fill the tank, or alternatively held as money. That is, if it’s a 120 barrel tank, and you’ve a minimum inventory of 20 bbl to have a buffer for regular customers — presumably you face high costs one way or another if you run totally dry, then you’d earn these yields on the dollar value of 100 bbl, depending on whether you emptied to make room for temporary storage, or filled to be ready for spikes.)
Of course, if the forward curve is very turbulent so that these trades are very profitable, presumably people would build more tanks, some of which would be full and some empty at any given time, reducing the spread volatility (sudden demands for oil or storage can be more easily accommodated), until the profitability of these strategies represents a “normal” risk-adjusted return on the capital invested in the tanks.
I’m thinking this through as I write, and I haven’t verified this in any way. I am very good at screwing stuff like this up. But, I gotta go… let me know if this seems to make any sense, or not. And, as always when I go on and on, blah, and sorry.
June 28th, 2008 at 9:35 pm PDT
link
groucho — I’m pretty sympathetic to your view. But it’s different than the momentum-driven, greater-fool speculative bubble (to which I was responding with that question).
If you think it’s a speculative bubble driven by uninformed fools, then it’s hard to answer why well-informed insiders don’t kill them by selling forward, without positing strategic behavior of some sort on their part.
If you think that the well-informed insiders don’t want dollars or euros or stocks or bonds anymore, then there’s really not much of a riddle why prices in terms of those things are very high.
My guess is much closer to the second than the first, yours as well I think.
June 28th, 2008 at 9:44 pm PDT
link
ddt — Thanks! That’s a very nice one. I’m looking it over now.
June 28th, 2008 at 9:48 pm PDT
link
Steve,
I’m not questioning the use of near-equilibrium models in itself (I’m physicist, I’ve been trained to see harmonic oscillators everywhere I look!) and I don’t claim that the current price action in oil is evidence of a bubble, I don’t know. What I know is that you can’t use near-equilibrium models to disprove the existence of a bubble, for the simple reason that there are no bubbles in a near-equilibrium world.
I agree with you that the deep reason for the run up in commodities is the weakened outlook of traditional financial assets, especially the dollar denominated ones. Converting today’s dollar into claims on future production of something real has become a serious investment theme in a world where the return ‘of’ capital is rapidly becoming more important than the return ‘on’ capital. Assuming future markets will not blow up, an investor who buy a future contract of oil is not that different from the one who buys an ounce of gold and buries it into his backyard. They both forego earning interests in order to avoid financial and currency risk.
I think the change in sentiment about traditional financial instruments is affecting both longs (investment and pension funds) and shorts (producers with a current account surplus), so if you want it is really a change in fundamentals and can last very long.
Finally, since future and spot prices can be arbitraged with risk-free schemes, is there really any reason to expect investment (speculative) demand to produce higher inventories? (that is until speculative demand doesn’t grow bigger than the production sell forward)
(I find the whole discussion very interesting and a demonstration that the internet really sets a new standard for public awareness about important economic issues.)
June 29th, 2008 at 4:32 pm PDT
link
I forgot to mention China among the longs (lot’s of dollars to trade against future production of real stuff)! That could be enough to explain how non-exchange traded commodities are booming as well.
June 29th, 2008 at 4:42 pm PDT
link
“Let me know if this seems to make any sense, or not”
Wow! This was a tough one to work through – a Sisyphus of convenient truth for a novice. You were correct that a search for symmetry was at the heart of my question. Let me reconstruct your explanation (which does make sense), and see if my version holds up:
Suppose an oil “volatility trader” has a starting position consisting of 50 per cent oil and 50 per cent unused storage capacity. His oil component consists of long spot oil/ short oil futures. His storage component consists of unused storage/ long oil futures. The futures positions at the outset effectively cancel on consolidation, assuming these positions are retained, but other combinations are possible in alternative strategies.
The trader’s opening portfolio thus is balanced with respect to his option to choose between one of two volatility trading strategies (or a combination of the two), based on upside or downside spot/futures spread volatility:
Strategy 1 (oil convenience yield) is based on the expectation of upside spot oil price volatility combined with relatively quiescent futures prices. Thus, he expects the spot/futures spread to widen, or move in the direction of less contango or more backwardization. He can choose the size of his exposure. He can remain with his current 50 per cent oil spread content or increase it up to 100 per cent. That depends on where he lies between neutral and aggressive on his upside volatility strategy. If the expected spread widening materializes, the trader can cover his oil position at a profit by selling spot and buying futures.
Positioning for strategy 1 puts upward pressure on the spot/futures oil spread by purchasing spot oil and selling futures. It makes it more expensive, which is natural if there is demand for the position from traders. The additional spread becomes a cost component that is defined as the oil convenience yield, and it is equivalent to an option premium (call option) on the spot/future spread. Conversely, the cost of the oil convenience yield causes the futures/spot spread to narrow. Thus, oil convenience yield is a subtraction from the expected return on spot oil (in the form of the futures/spot spread).
Strategy 2 (storage convenience yield) is based on the expectation of downside spot oil price volatility combined with relatively quiescent futures prices. Thus, the trader expects the spot/futures spread to widen, or move in the direction of more contango or less backwardization. He can choose the size of his exposure. He can remain with his current 50 per cent unused storage capacity or increase it to 100 per cent. That depends on where he lies between neutral and aggressive on his downside volatility strategy. If the expected oil spread widening materializes, the trader can cover his unused storage position by buying spot oil and selling oil futures.
Positioning for strategy 2 puts downward pressure on the spot/futures oil spread by selling spot oil and purchasing futures. It makes it cheaper. But the trader is selling rather than buying this spread, so this reduced spread becomes a cost component that is defined as the storage convenience yield, and it is equivalent to an option premium (put option) on the spot/future spread. Conversely, the effect of the storage convenience yield is to cause the futures/spot spread to widen. Thus, storage convenience yield is an addition to the expected return on spot oil (in the form of the futures/spot spread).
(A combination of strategies 1 and 2 becomes an option straddle – calls and puts together.)
These oil and storage convenience yield effects are consistent with the following equations:
Interest rate – oil convenience yield = forward yield
Interest rate + storage convenience yield = forward yield
Storage convenience yield – oil convenience yield = 2*[forward yield – interest rate]
These are the same as your equations.
(I have not yet worked through your subsequent numerical calculations.)
Finally, the symmetry of the two strategies suggests that unused storage is conceptually equivalent to a short oil position. This is not intuitively obvious to someone unfamiliar with the subject. It’s something I had considerable difficulty with in replicating the model to my satisfaction. But the upside volatility trader wants to hedge his directional oil risk by selling futures. And the downside volatility trader wants to hedge his directional storage capacity risk (i.e. the risk of not filling it with oil eventually) by buying futures. To the degree that unused storage capacity represents this kind of risk, it is equivalent to a short spot oil position, and can be hedged in this way.
Your detailed feedback is much appreciated. Thanks again.
June 29th, 2008 at 9:19 pm PDT
link
follow up, fyi:
Marc Thoma has been developing an oil supply/demand model that includes both flow and stock (inventory) components. He’d gotten to the point of integrating convenience yield into the inventory model in yesterday’s post “Another Iteration on the Speculation Model”. I registered the following comment, regarding the oil convenience yield part (not storage convenience yield):
……..
Some thoughts:
a) The nature of the “convenience” in question as I understand it is that it allows traders to pursue profit seeking strategies by exploiting pure volatility of expected returns (based on the spread between spot and futures prices) with option related strategies. Steve Waldman describes some of these strategies in his post.
b) The value associated with this convenience is in the form of an up-front capitalized cost that is in effect a subtraction from what would otherwise be the spread between spot and futures prices. This up-front capitalized cost, the “convenience yield” is really an embedded option premium that is de facto extracted from the return that otherwise would have been expected by non-trading hedgers and speculators.
c) “Convenience yield”, as an option premium, is both the cost of entering these trading strategies, and the market’s best determination of the expected risk adjusted profit arising from them. The actual yield to the trader isn’t determined until the option has been exercised or expired. And like any long option strategy, a trader must first earn back his premium expenditure before turning net profits. Traders will eventually realize some gross return on their investment, which will either be equal to, less than, or more than their initial premium investment.
d) Convenience yield has a subtractive effect on the expected speculative/hedging return from holding oil otherwise. Therefore, the total expected return from holding physical oil is the expected holding period return typically sought by hedgers or non-trading holding period speculators/arbitrageurs, plus the convenience yield, which is the value of the option and the corresponding capitalized value of expected returns for volatility traders. This decomposition corresponds conceptually to the sum of a “delta” (linear) return plus a “volatility” (non-linear) return.
………
June 29th, 2008 at 9:42 pm PDT
link
I was wondering of any of the tricks that Enron did with electricity might be involved here. For example Enron bought electricity from California, created a shortage by shutting down some of their power plants and then reselling the electricity back at a higher price. So they didn’t need to store any inventory to do this.
So say a country like China or India contracts for a large amount of oil, perhaps more than they really need and signal to the market they expect to need a lot more next year. They also agree to buy some of this oil at much higher prices to give the impression they will be prepared to pay this price or more next year. Because they haven’t received the oil yet they don’t need to store any oil to create a shortage.
So their average price of oil ends up below the market because the bulk of their purchases, say through the futures market were at lower prices. It was only perhaps the last 10% of their purchases that looked like they were willing to pay these high prices. Then when prices go right up they sell some of this oil, which they never received and did not have to store at the higher prices and make a profit. They might even prick the bubble themselves later so they can buy cheaper oil later, and make money by shorting the price.
Speculators could also do this by acting for someone like China or even for themselves. Enron did it without using the power themselves. The result would be much higher prices without anyone using much more oil than they did with the lower prices.
They could also make purchases to make it appear they were buying for a government e.g. China. For example if China needed extra oil or announced it was going to make some more buys then the speculators would anonymously make large buys and spread around the rumour it was the Chinese.
So if Enron managed to cover their tracks how do we know someone else isn’t doing this, particularly with the high volume in the oil futures market?
June 30th, 2008 at 12:30 am PDT
link
Anon
I have a problem with these equations
Interest rate – oil convenience yield = forward yield
Interest rate + storage convenience yield = forward yield
I believe they imply the if oil convenience yield is positive then storage convenience yield must be negative. I thought both had to be positive?
Also, conceptually, unless you have a monopoly on storage space in a given market, you should never be able to earn a return on storage from buying spot and selling forward that exceeds the interest rate. So I’m having a problem with the convenience yield on storage argument. Or maybe I’m just confused.
June 30th, 2008 at 7:43 am PDT
link
MG:
Judging from earlier comments, you’re more familiar and comfortable with this subject than I am. More probably I’m the confused one – but hopefully not way, way off.
I did get bogged down with the equations, but somehow managed to generate the same one Steve did by adding the two in question. Doesn’t mean these equations are right – could be a coincidence. I posted my comment after reaching critical maximum brain amp on the subject. So I don’t have a response right now.
You may well be entirely right. As I said, I’ve found the entire storage convenience yield concept difficult. I’ll have to spend a little more time on it. I should be able to return with a rehash in the next few days; perhaps I’ll post something additional in case you’re interested. Any other insights you have are appreciated.
June 30th, 2008 at 9:09 am PDT
link
My story is more dollars chasing relatively inelastic short-run supply–no increase in inventories necessary. But I must insist this is only a story, as this is not my area.
See John Mauldin’s presention of a piece by Louis Gave on world-wide inflation trends for circumstantial evidence supporting my story (I think) and also predicting the commodity inflation is about to roll over.
June 30th, 2008 at 9:51 pm PDT
link
MG:
I believe the equations in question are correct:
Interest rate – oil convenience yield = forward yield
Interest rate + storage convenience yield = forward yield
The re-work follows (this is pretty long):
Let:
p = oil spot price
f = oil futures price
i = interest
Then, apart from convenience yield of either type or storage cost of normal type, arbitrage suggests:
f – p = i
i.e.
forward yield = interest (or interest rate when expressed in terms of 1/p)
Oil Convenience Yield
The convenience yield on oil is the expected profit from trades that are expected to benefit from upside volatility in spot oil and the spread (p – f). The trader puts on a position of long spot oil, short oil futures. The short futures position hedges the long spot position against directional downside price risk. In option terms, the trader is long spot volatility, short future delta. The trade is long the spread position (p – f), which is the same as short the spread position (f – p), or short the forward yield.
Since the trader is short the forward yield, he profits if volatility reduces that spread – i.e. if volatility moves the spread marginally in the direction of backwardation.
There are three sources of price impact associated with this trade, all of them driving the spread in the same direction:
a) Marginal backwardation associated with putting on the marginal trade (long spot; short futures)
b) Cumulative marginal backwardation associated with the degree to which the trade is “in the market”
c) Expected future marginal backwardation associated with any individual trader’s proprietary view of the spread, and his expectation that the future spread will moved favourably beyond what is already reflected in market pricing
The degree to which forward yield arbitrage is affected by oil convenience yield at any point in time is an indicator of effect b) above. Oil convenience yield in and of itself reflects the expectation of positive spot price volatility and negative forward yield volatility. It is in the market as the equivalent of the premium on an embedded put option on (f – p); i.e. an embedded call option on (p – f). The cost of the option premium (invested by traders) marginally backwardizes the (f – p) spread, and the trader expects to gain from an extension of that move.
So the new arbitrage, including the effect of oil convenience yield, is:
Forward yield = interest rate – OCY (marginal backwardization effect)
Storage Convenience Yield
The convenience yield on storage is the expected profit from trades that are expected to benefit from downside volatility in spot oil and the spread (p – f). The trader has access to unused storage capacity in order to be able to buy spot oil after it spikes downward. The trader puts on a spread position of short spot oil (i.e. unused storage capacity), long oil futures. The long futures position hedges the short spot position against directional upside price risk. In option terms, the trader is short spot volatility, long future delta. The trade is short the spread position (p – f), which is the same as long the spread position (f – p), or long the forward yield.
Since the trader is long the forward yield, he profits if volatility increases that spread – i.e. if volatility moves the spread marginally in the direction of contango.
There are three sources of price impact associated with this trade, all of them driving the spread in the same direction:
a) Marginal contango associated with putting on the marginal trade (short spot; long futures)
b) Cumulative marginal contango associated with the degree to which the trade is “in the market”
c) Expected future marginal contango associated with any individual trader’s proprietary view of the spread, and his expectation that the future spread will move beyond what is already reflected in market pricing
The degree to which forward yield arbitrage is affected by storage convenience yield at any point in time is an indicator of effect b) above. Storage convenience yield in and of itself reflects the expectation of negative spot price volatility and positive forward yield volatility. It is in the market as the equivalent of an embedded call option premium on (f – p); i.e. an embedded put option premium on (p – f). The cost of the option premium (invested by traders) effects marginal contango on the (f – p) spread, and the trader expects to gain from an extension of that move.
So the new arbitrage, including the effect of storage convenience yield, is:
Forward yield = interest rate + SCY (marginal contango effect)
I think this should answer your first question, which was:
“I believe they imply that if oil convenience yield is positive then storage convenience yield must be negative. I thought both had to be positive?”
Both types of convenience yield are positive, as they represent long option premium investments that are expected to deliver positive returns to the respective trades. But as explained above, an oil convenience trade puts downward pressure on forward yield because it is a bet on marginal backwardization, and a storage convenience trade puts upward pressure on forward yield because it is a bet on marginal contango.
In summary, both of the equations in question appear to be correct:
Interest rate – oil convenience yield = forward yield
Interest rate + storage convenience yield = forward yield
Your second question was:
“Also, conceptually, unless you have a monopoly on storage space in a given market, you should never be able to earn a return on storage from buying spot and selling forward that exceeds the interest rate. So I’m having a problem with the convenience yield on storage argument. Or maybe I’m just confused.”
I haven’t considered this question to the same extent as the first. But I can’t see anything in the conceptual model that constrains positive yield expectation as a function of interest rates. The convenience yield on storage as defined represents the opportunity for strategies that take advantage of downside volatility in the spot oil price (and upside volatility in the forward yield). Those with unused storage have a number of strategy choices. They can employ storage convenience strategies as defined, which involve opportunistic volatility trading – essentially waiting to buy spot on a downside spike and then covering on reversion. A second strategy choice, assuming the forward yield offers an arbitrage opportunity, is simply to buy spot and sell futures, holding that position to the futures date, and locking in arbitrage profit on the oil thus purchased and stored. But it is the activity of those executing the first strategy – i.e. waiting for volatility opportunities while hedging with futures – that can cause this “mispricing” opportunity for those executing the second strategy. The two activities are diametrically opposed in terms of marginal pricing effect. The question is which one is stronger at the margin. Finally, a third strategy is that those with unused storage capacity presumably can ‘rent’ it out, although I have no idea how this market works. Perhaps that’s the activity you refer to when you say such operators shouldn’t be able to earn more than the interest rate. I don’t know.
An additional aspect may be relevant, although I’m not familiar with the economics of storage costs, so I’m guessing here. Suppose there is some fixed cost associated with owning storage capacity, regardless of capacity utilization – something like “owner’s equivalent rent” in residential real estate. And suppose some traders actually rent storage as inferred above when needed. The arbitrage equatio
n might take these types of costs into account. If so, oil or storage convenience costs should then be viewed net of such storage cost. But that just requires tweaking the cost structure of the model a bit.
Finally, I’ll return to my own original question that sparked the discussion on storage convenience yield. Are negative convenience yields possible?
You and Steve responded immediately with the answer that’s taken me several days to work through – which was that a negative oil convenience yield is more easily thought of as positive storage convenience yield. But unused storage is conceptually equivalent to a short spot oil position. Therefore, a negative oil convenience yield can also be thought of intuitively as a short position in oil convenience yield that is associated with a short position in spot oil. This becomes even more intuitive when one considers that a trader with a position in storage convenience yield (i.e. betting on downside oil spot volatility and upside (f – p) volatility) is effectively trading against, or shorting, the view of a trader with a position in oil convenience yield.
July 1st, 2008 at 12:32 pm PDT
link
Anon:
Thanks for your extensive post. I have spent some time thinking about it. I feel I have a good handle on the oil convenience yield. You store oil and sell forward hoping for the spread to widen in favor of the spot. You try to sell at the maximum spread and close out the futures position (exercising the option). If the spread moves against you, the worst case is you deliver the oil against the futures position. The cost is the premium you paid for spot over the futures price net of holding costs. So far so good.
Now the other trade: you sell oil and take a long futures position and you earn some interest on your cash position. In this case, exercising the option means buying back spot and closing out the futures position. When does it pay to exercise? It’s not enough for the spread to move in your favor. Unless spot moves below the futures price net of holding costs, you are better off earning interest on your spot sale and taking delivery of the futures position. But, unless storage is full (or you control all of it), the spot price will never get that low, because anyone with spare storage can earn a risk-free return by buying spot and selling forward. Therefore, the option is never exercised and has no value. I think. Sorry for beating a dead horse.
July 1st, 2008 at 6:27 pm PDT
link
MG:
“The spot price will never get that low, because anyone with spare storage can earn a risk-free return by buying spot and selling forward.”
You may be right in part or in whole. I don’t know. But a counterargument exists that contradicts such an inference.
Your point is consistent with the idea that the market is more efficient in arbitraging away potential profit opportunities on the storage convenience trade than on the oil convenience trade. The implication is that realized spread volatility is always skewed; i.e., realized volatility offers trading opportunities in one direction (oil convenience), but not in the other (storage convenience).
If an arbitrage exists that is inverse to the one you’ve described, it would suggest that we can expect similar levels of intensity of both arbitrage and more aggressive volatility trading on either side of the curve. There would be no reason to expect a skew in realized volatility, or to expect volatility trading opportunities for oil convenience yield while not expecting them for storage convenience yield. Conversely, there would be no reason to expect any less dampening of volatility opportunities due to ongoing arbitrage in oil convenience than there would be for storage convenience.
Such an arbitrage does exist on the oil convenience side. You’ve described the arbitrage that seems natural on the storage convenience trade. The strategy over the entire holding period comprises an investment in cash, at the risk free rate, with an option to exit cash into a fully hedged investment in oil, resulting in a risk free return that exceeds the risk free rate. But the inverse arbitrage opportunity exists on the oil convenience side. This consists of a fully hedged investment in oil, at the risk free rate, with an option to capture excess return through arbitrage, and exit oil into risk-free cash.
Assume the investor faces a neutral or fully-arbitraged oil curve at the outset. The curve by definition is in contango, with the forward yield covering interest and storage costs. You’ve alluded to the arbitrage that one might expect to occur immediately if the contango accentuates. The investor buys spot oil and sells futures in order to capture excess forward yield on a risk free basis. He exits cash and move into fully hedged oil.
Now suppose the same investor adopts the inverse strategy at the outset. Since the curve is fully arbitraged, he can buy oil and sell futures immediately and capture the risk free rate of interest. Then, like a volatility trader, he waits for curve volatility. If the curve contango compresses and moves in the direction of backwardization, the investor closes his position at a profit, just like a volatility trader. He exits oil and moves into cash.
The investor captures this excess return when he closes his spot and futures positions. He realizes this gain as the net result of these two components. This net gain translates to the present value of a yield pick-up over the remaining holding period for the combined oil/cash investment. Depending on the degree of movement in the curve, the investor captures profit translatable to excess return over the remaining period, as happens directly in storage convenience arbitrage.
Both types of investment are risk free. The order of cash and oil is merely reversed. In either case, the investor must define a holding period that is determined by the date of the futures contract prospectively used in the oil investment component. This is a parameter that makes holding periods comparable. Then the excess return in either case is defined by the timing of the arbitrage execution (i.e. the remaining time to the end of the holding period) and the amount of spread profit that is captured in the arbitrage. Spread profit in storage arbitrage is inherently amortized over the contract life of the concluding oil investment. Spread profit in oil arbitrage is translatable to an equivalent amortization of excess return over the remaining holding period for cash, as defined by the expiry date of the futures contract used in the front oil investment component. Given the comparable nature of these arbitrages as inverses of each other, there is nothing to suggest that one should have a biased advantage over the other in terms of either their timing or the amount of spread or excess return that is captured. These arbitrage opportunities on either side of the curve are just mini-versions, or buy and hold investment versions, of the more aggressive volatility trading strategies already discussed. There is no reason not to expect such strategies to be operating without bias on both sides of the curve.
July 2nd, 2008 at 8:34 am PDT
link
Anon:
Last word (I promise). You have convinced me about the symmetry of the trades. Here is where I made my mistake. When I said that it would never pay to close out the short storage long futures trade, I failed to take into account that when you repurchase the oil, you are also buying back the oil convenience yield as well. So you would be willing to pay a premium over the futures net of holding cost.
Thank you for an enlightening discussion and apologies to Steve for hijacking this thread.
July 2nd, 2008 at 11:36 am PDT
link
According to this link the oil price is completely based on futures so that demolishes the argument speculators are not involved:
peakoil.debunked.blogspot.com
“The declining liquidity of the physical base of the reference crude oil and the narrowness of the spot market have caused many oil-exporting and oil-consuming countries to look for an alternative market to derive the price of the reference crude. The alternative was found in the futures market. When formula pricing was first used in the mid-1980s, the WTI and Brent futures contracts were in their infancy. Since then, the futures market has grown to become not only a market that allows producers and refiners to hedge their risks and speculators to take positions, but is also at the heart of the current oil-pricing regime. Thus, instead of using dated Brent as the basis of pricing crude exports to Europe, several major oil-producing countries such as Saudi Arabia, Kuwait and Iran rely on the IPE Brent Weighted Average (BWAVE).11 The shift to the futures market has been justified by a number of factors. Unlike the spot market, the futures market is highly liquid which makes it less vulnerable to distortions. Another reason is that a futures price is determined by actual transactions in the futures exchange and not on the basis of assessed prices by oil reporting agencies. Furthermore, the timely availability of futures prices, which are continuously updated and disseminated to the public, enhances price transparency.
[11] The BWAVE is the weighted average of all futures price quotations that arise for a given contract of the futures exchange (IPE) during a trading day. The weights are the shares of the relevant volume of transactions on that day. Specifically, this change places the futures market, which is a market for financial contracts, at the heart of the current pricing system.”
Also here is a good example of speculators at work:
commoditytrader.com
July 4th, 2008 at 1:01 am PDT
link
Steve – you’ve correctly cited the classic cost of carry model for a unbiased forward price. But it does not include investor risk premium. The observed price is biased by investor risk premium (supply/demand for the forward contract, if you like). Your statement “When a storable commodity like oil is in backwardation, that doesn’t mean that the markets are predicting that its price will fall” is misleading. It making the assumption that a forward price must reflect an unbiased estimate of the expected future spot price, you’ve given the convenience yield too much work (i.e., you are bundling investor risk premium with the convenience yield). The theory of normal backwardation (not backwardation) refers to a F < expected future spot exactly because investor have risk premiums.
July 6th, 2008 at 12:04 pm PDT
link
Econophysics weighs in with good old supply and demand
July 7th, 2008 at 6:45 pm PDT
link
Here is the arxiv link
“In conclusion, the present study supports the hypothesis
that the recent oil price run-up, when expressed in
any of the major currencies, has been amplified by speculative
behavior of the type found during a bubble-like
expansion. The underlying positive feedbacks, nucleated
by rumors of rising scarcity, may result from one or several
of the following factors acting together: (1) protective
hedging against future oil price increases and a
weakening dollar whose anticipations amplify hedging in
a positive self-reinforcing loop; (2) search for a new highreturn
investment, following the collapse of real-estate,
the securitization disaster and poor yields of equities,
whose expectations endorsed by a growing pool of hedge,
pension and sovereign funds will transform it in a selffulfilling
prophecy; (3) the recent development since 2006
of deregulated oil future trading, allowing spot oil price
to be actually more and more determined by speculative
future markets [19] and thus more and more decoupled
from genuine supply-demand equilibrium.”
July 7th, 2008 at 9:00 pm PDT
link
Iran/Israel/USA saber rattling threatens significant production shortages since 16.5-17 million bpd travel through the Strait of Hormuz (2006 EIA numbers). This should cause increased convenience yield since oil producers outside the Persian gulf selling on the future market miss out on the resulting oil super duper price spike.
July 10th, 2008 at 9:22 am PDT
link