When you’re abducted by aliens, there’s little cause to be cynical. The sucktitude of a painful probe is straightforward. There’s no sugarcoating to see past, things are exactly as bad as they seem. Between the screams you realize that, in a way, you have been offered a kind of innocence. When you are abducted by aliens, you savor the silver linings.

After such an ordeal it’s a bit depressing to be dropped off on the Planet of the Covered Bonds. Cynicism levels are off the tricorder here as, alas, they should be. [See Yves Smith, Michael Shedlock, Maxed Out Mama. Less cynically, David Merkel offers a very nice description of what covered bonds are and how they work.]

Covered bonds sound nifty. They’re designer drugs. They’re just like the mortgage-backed securities that gave us such a fine party, except the nasty hangover inducing components have been engineered away. They are on-balance sheet loans, look Ma, no Enron! (finally…) Covered bond issuers have “skin in the game”, skin, bone, and sinew actually, as they guarantee the loans. That problem of “misaligned incentives” is solved, ‘alleleujah! (…though intrafirm agency problems are not addressed.) These are old-fashioned, full recourse, secured and overcollateralized loans, just packaged into tradable securities. What could possibly go wrong?

Formally, the only way anything could go wrong would be if the issuing bank fails and the pledged assets turn out to be worth less than originally estimated. Do you think those two events might be correlated? Covered bonds can certainly be no worse, from an investor standpoint, than the nonrecourse asset pools they are intended to replace. A guarantee by the issuing bank has gotta be worth something. If it were 2002 again and the banking industry had adopted this originate and guarantee model (rather than the originate and forget model they chose), perhaps we wouldn’t be in the current mess. But it is not 2002. These bonds will be offered by banks that would already have collapsed without vast support to the financial system by the Fed and the US Treasury. Guarantees by money-center banks are no longer bonds of confidence in the prudence or skill of bank managers. The value of such guarantees comes from a different place, from the notion that it is unthinkable the state would permit these banks to fail. A covered bond offered by Citi or Bank of America would only default if a titan collapsed. Investors might reasonably believe that would not be permitted to happen. If they are right, then these bonds are indeed covered. They are covered by you, dear taxpayer.

The great credit crisis of 2007-2008 is slouching towards its Bethlehem, a full faith and credit crisis for the United States of America. This die was cast at the first TAF auction, when the Fed chose to pull private credit risk onto taxpayers’ already strained balance sheet, rather than endure any unpleasantness. Covered bonds may prove to be a success with investors. But, careful what you wish for. The more banks sell, the more we’re all on the hook, if the loans go bad. Covered bonds issued by “too big to fail” banks are basically equivalent to mortgage backed securities guaranteed by Fannie and Freddie. It’s just another way of putting private-sector bells and whistles on a public sector assumption of risk.

These bonds are seen as a way of “unfreezing the housing market”. The housing market seems frozen because in many areas, relationships between home prices, rents, and incomes are still out of whack. Assuming relatively stable rents and incomes (bad assumption, I know), mortgages in “stuck” markets made at or near current asking prices are likely bad investments. That suggests the implicit taxpayer guarantee won’t expire unused. The more covered bonds are sold, the more extreme measures or hidden subsidies will be required to prevent household names from failing.

The committee to save the world is you, and we will be grateful for your contribution, although we will never thank you, or admit that anything other than the skill of our red knuckled, fabulously wealthy financiers had anything to do with the eventual recovery. That period of commodity inflation and steep yield curves was just a market outcome, a fact of nature. Of course our proud financial institutions were always going to weather the storm. They are the best and most sophisticated in the world. Thank goodness for private enterprise.

[HT Yves Smith on the slouching towards Bethlehem thing. BTW, my use of the term “taxpayer” is imprecise, state guarantees are really backed by “taxpayers and/or those most vulnerable to inflation (low bargaining power workers and those on fixed incomes)”. My guess is that we will use tradables inflation more than outright taxation to save the whales. FD, I’m short long-term Treasury futures and long precious metals, going with that whole full faith and credit crisis scenario. As always, this ain’t investment advice, I frequently lose my shirt so go copy Warren Buffett or something.]

Update: Felix Salmon directs us to an excellent new blog on which John Hempton writes:

[I]f you have lent to people in a currency where interest rates suddenly go to 50 percent (as happens in some devaluation crises), your funding cost (deposits) will rapidly go to 50%. However if you pass that on to your borrowers they will fail. You will suffer credit risk and possibly go insolvent. If however you have offered fixed loans to your borrowers you will wind up with huge funding mismatches – and possibly go insolvent. For small moves there is a difference between credit risk and interest rate risk. For large moves there is no effective difference. The same analysis applies to currency and credit risks.

This goes some way towards adressing Tyler Cowen’s demurral…

I cannot see that the credit of the United States government is in danger. There is a) the printing press, and b) our location on the left side of the Laffer Curve.

I agree with Tyler that the US government is more likely to print than default outrught, if those are the alternatives (though do recall this from the generally levelheaded Accrued Interest). But, for large moves, I think the distinction between credit risk, inflation risk, and currency risk is largely academic. (Regarding Tyler’s second point, Robert Olson hits the nail on the head in a Marginal Revolution comment, “Being on the left-side of the Laffer Curve doesn’t matter much if the political situation makes it impossible to raise taxes.”)

Err… is this thing on? Am I back?

I think I’m back.

I am periodically abducted by aliens, who do unspeakable things the details of which I can only guess from various aches and irritations.

In my absence, the comments on the previous more-than-a-month-ago post were remarkably good. The blog is better, actually, when I disappear. Smarter voices chatter.

The whole oil thing seems so, like, last month, although I notice there was some kind of deadhead revival in SoCal a couple of days ago. Some quick, crude thoughts: the whole “fundamental” vs “speculative” debate is terribly miscast, as emphasized most recently by Jeff Frankel (via Mark Thoma), but also by Tyler Cowen, and me too. What I liked best about the Thoma / Krugman model is that it gave us four lines to think about, two kinds of demanders (people who want to burn oil vs people who want to store it) and two kinds of suppliers (people who suck oil from the ground vs people who drain their tanks). An imbalance of speculation on futures (more longs than shorts) creates incentives for people with tanks to fill them, potentially shoving up one of the two demand lines (the one on the left-hand panel of the Thoma/Krugman graphs). But four lines iz a lot of moving parts. I think the really interesting line is the right-panel supply line. Rather than “speculation” vs “fundamentals”, I wonder whether discretionary oil producers are flat-out producing as much as they are able, given the infrastructure currently in place, and whether over the past few years they have held back on developing capacity, or whether they are in fact eager to pump but hitting “peak oil” limits. Either story is consistent with James Hamilton’s fundamentals, although one might call unenthusiastic production “speculative” in a certain sense. In the end, I think Paul Krugman wins the debate he started, if it was the left-panel demand line driving prices, the only piece futures-buyers can influence, we should observe storage in tanks. As both Robert Waldmann and Alea’s jck (in a comment) point out, paper speculators only persuade oil producers to leave the stuff in the ground when they drive futures into something close to strict contango, because producers enjoy less of a convenience yield than people with tanks. Inventory should build in tanks before it builds underground, if increased stock demand is driving the story.

It’s important to note that, just because futures buying / speculative storage probably did not drive the great oil price boom of early 2008, doesn’t mean it could not affect prices. Imagine, in Mark Thoma’s discussion, that rather than a parallel outward shift in demand, the slope of the stock demand curve flattens as well. The “flatness” of stock demand maps to speculators’ conviction that prices will rise. If speculators are absolutely certain that (the present value of) future prices will be higher than the current price, then they would persistently buy as much as would be necessary to pull the flow market price to the expected future price. In Mark’s scenario, speculators effectively choose a quantity they are willing to buy at above the spot clearing price, and prices revert once their appetite has been sated. But speculators might choose price rather than quantity. (Still, if they do, we should see inventory build.)

Of course, explaining the rise in oil prices is passé. Now it’s all about explaining the fall. Is it demand destruction? an incipient long run? declining inventories? increased production? a speculative bubble going “pop”? I dunno. Do you? (Maybe it’s those evil short-sellers.)

In the month-ago discussion, Arnold Kling was the first to point out the connection between option values and the convenience yield. That theme was developed quite extensively by commenters, especially anon and MG, and is common in the academic literature as well. The kind of option a convenience yield represents is fun to think about. It is an option whose underlying is fluctuating calendar spreads, rather than prices. There is a lovely symmetry, in that there is a positive convenience yield both on having the commodity available, and on not having the commodity (but having an place to efficiently store it). If that seems weird, recall how same-strike call and put options both have positive value, even though when one is in the money, the other cannot be. We can even derive a relationship between the expected value of these two convenience yields somewhat analogous to put/call parity.

This all seems very retro now, a month is a long time, in the blogosphere and in financial markets. If I can avoid the lights in the sky, perhaps I’ll come up with something more exciting to write about soon.

Oh! Speaking of exciting, welcome Gabriel!

If a commodity is in “backwardization”, that is, if futures prices are lower than current prices, does that imply that futures markets are discouraging storage (encouraging disgorgement)? Paul Krugman makes the case, here and here.

I’m going to challenge him with a low-down, dastardly kind of argument. The gentleman keeps asking for evidence, evidence, and in response I’m going to offer an unfalsifiable hypothesis. Krugman says that futures prices are too low to cause people to withhold physical oil and sell forward, as required to affect spot prices. But whatever forward price curve he shows me, I can posit an invisible “convenience yield” large enough to make hoarding oil worthwhile. I don’t even have to be unreasonable about it. Extrapolating from historical data, we see that gently “backwardized” futures prices might be quite sufficient to encourage storage when convenience yields are taken into account.

Despite all of this, I agree with Krugman that futures markets can’t explain the recent skyrocketing oil prices. Not unusually, he’s been a voice of sanity and reason. But just as speculation in futures need not affect spot prices (if it is balanced long and short), speculative withdrawal of physical supply need not affect the shape of the future price curve. Futures market “signatures” can’t be relied upon to distinguish speculative from fundamental demand, and inventory may be unmeasurable, especially if it is offshore or takes the form of withheld production. Further, both futures in contango and measured inventory build can signify known fundamental demand as well as speculation. (Suppose entrepreneurs are planning to fire up many new factories over the next few months. If they buy forward to hedge their exposure to energy prices, that would push futures into contango and promote storage with no one speculating on anything.)

But this isn’t about that. This is a disquisition, and ode, a homage and a tribute to the marvelous, mysterious, misunderstood and maligned convenience yield:

The bedrock principle of futures markets is “no arbitrage”, that is prices should be set such that there is no investment strategy that yields a risk-free profit higher than the risk-free rate of interest. For a physical commodity, this seems to imply that the forward price should equal the present price plus the risk-free rate of interest and any storage costs. Interest rates are never negative, and storing stuff always costs something, so you’d expect future prices of storable commodities to always be higher than current (“spot”) prices. But check out the following graph of the four month “forward yield” of crude oil. (Data courtesy of the EIA, hat tip Krugman, calculations and errors are mine, click for a bigger version).

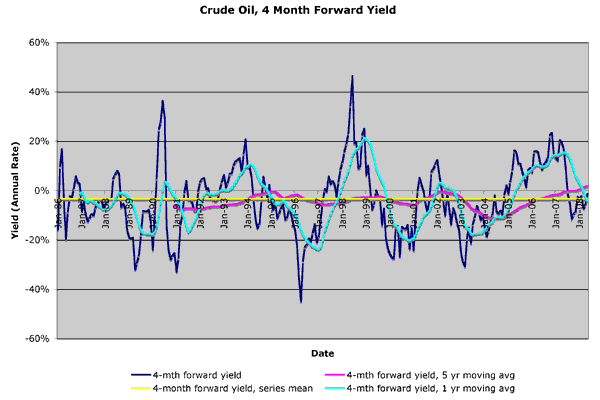
The “forward yield” is just the percentage by which the future price is higher than the spot price. I’m using four month futures, but I’ve converted the yield an annual rate. If the forward yield is 10% and the interest rate is 4%, an oil man would profit from buying oil now and selling it forward, as long as his storage costs are less than 6% per year. Tycoons would start buying spot and selling forward until yield dropped to interest + storage.

But didn’t we say future prices should be higher than spot prices? Look at the average (the yellow line in the graph). It at -3.4%, well below zero! The yield is negative more often than it is positive. Whenever the yield is anything less than interest + storage, you’d expect oilmen to sell crude from storage and buy it back forward. He earns interest on his cash and saves the storage costs that way, which is better than the profit he’d make storing and selling forward. When the forward yield is negative, Texans should be selling physical and buying forward like mad. By doing so, they earn interest on cash, save storage costs, and lock-in an easy profit buying back their oil for less than than what they sold it for. Very quickly, all the selling should create a glut of physical oil, driving down spot prices, while the buying forward drives up future prices, until the yield is positive and sanity is restored. But negative forward yields for oil have persisted, sometimes for years at a time! We must be missing something. Hmmm…

Suppose someone offered to buy your vacuum cleaner today for $100, and sell it back to you next week for $80, with no risk of wear or breakage. Would you? It would depend how much you value the use of your snorter. If you refuse, we might infer that a week’s access to the pleasures of vacuuming is worth 20 bucks to you. We call that value of temporary use a “convenience yield”. It’s as if having the vacuum cleaner around pays you $20, even if no cash changes hands. Maybe we observe negative forward yields on oil because the smell of oil in the morning is priceless to guys in cowboy hats. (Or not… see below for a more plausible account of oil’s “convenience yield”.)

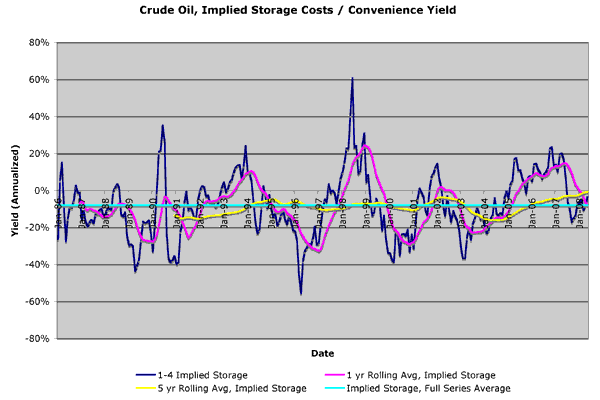
Let’s eliminate wandering interest rates, and take a look at the storage cost / convenience yield of oil historically. Below is a graph of a three-month forward yield (calculated from the first to the fourth month forward, because futures prices are more trustworthy than spot) with the concurrent 3-month T-bill rate backed out of it, leaving only storage costs. When storage costs are negative, that reflects, by definition, a convenience yield. (Again EIA monthly data, T-bill rates courtesy of FRED, my calculations)

From Jan 1986 through May 2008, oil futures have reflected a convenience yield of 8% per year on average. (This is in rough agreement with the overall mean of 0.021% per day calculated here by Milonas and Henker, see Table 3.)

Suppose that the current convenience yield is about 8% and three month interest rates are about 2%. Then a one-year futures contract should be about 6% cheaper than spot, and a four-month-out contract should be about 1.4% cheaper than a one-month-out contract (reflecting 3 months of storage). At the end of May, the 4-month-out contract was in “backwardation”, but was only 0.5% cheaper than the 1-month, still too expensive given the convenience yield. Oil dudes could have earned (on an annualized basis) about 3.6% more than the risk free rate (about 5.6% overall) buying high and selling low, but enjoying the privilege of storage. Now that oil is in gentle contango (as of June 17, the 4 month contract costs about 1% more than the 1 month), buying forward and storing looks like a really fantastic deal.

What is this “convenience yield”? Is it real? It seems like it must be, the economics of an 8% return aren’t subtle in the data. But when I first encountered this idea, it baffled me. So instead of talking oil, let’s talk hotels.

Suppose you have a hotel, it’s morning, and you’ve got a room that isn’t yet booked for tonight. Empty rooms end up costing you about $10 a night, considering your rent, maintenance, utilities, etc. But, you estimate there’s about a 50% chance that a weary last-minute traveler will come by and pay your walk-in rate of $150 for the room. So, the risk-neutral expected value of your empty room is $65 [(150 ÷ 2) – 10]. You’re risk-averse, not risk neutral, though. You’d accept a certain $60 rather than a 50-50 chance of losing $10 or earning $140. That $60 is the “convenience yield” on your empty room, it’s what having a room empty, in case opportunity strikes, is worth to you.

Oil is a “spiky” commodity. Every once in a while, someone really needs it, now, and will pay a premium for immediacy. The market for oil in Cushing, Oklahoma might be reasonably efficient, but what happens when someone in Peoria needs oil today? Opportunity! Instead of running a hotel, you build an oil tank in Peoria. Suppose that every month, there’s a 10% chance a desperate client will offer a 5% premium for immediate delivery of all your oil, and that interest and storage cost you 0.2% per month. Then on average, you’d earn 0.5% (10% x 5%) each month from desperate clients, and pay 0.2% in expenses. You don’t want to bear the risk of fluctuating oil prices, so you sell your oil forward. If you were risk neutral, you’d be willing to sell it for a discount of up to 0.3% less than you bought it for at the beginning of the month, at which price you’d just break even. But you’re not risk-neutral: You attach a “certainty-equivalent” value of only 0.4% to the unpredictable income from needy customers, and would offer no more than a 0.2% discount on month-forward oil sales. In the end, you earn a risk-adjusted 0.4% per month “convenience yield” from desperate polluters, and pay 0.2% in interest and expenses, and 0.2% in hedging costs. If one-month oil futures pay more than 0.2%-less-than-spot, or (golden days!) if they are in contango, you’d buy as much oil as you could and sell it all forward, because every new barrel that you promise to buy high and sell not-so-low represents certain (well, “certainty equivalent”) profit.

Putting aside Peoria and our artificial needy customer, sometimes oil spikes even on the wider market, so that anybody with physical oil can sell at a high price and while locking in low-priced near future purchases to replenish their stock quickly enough to meet any other contractual obligation to sell. If you estimate the profit you’d to earn from these occasional opportunities, and subtract a bit to come up with a “certainty-equivalent” value for this uncertain income stream, you’ll have determined a convenience yield. It shouldn’t be surprising that convenience yields are especially high for volatile commodities subject to frequent shortages and price spikes.

When futures markets are well-arbitraged (which might not always be the case!), the future price of a storable commodity is determined by the spot price plus the total cost of storage, defined as foregone interest, plus storage costs, minus any benefit of temporary ownership &mdash the convenience yield! When a storable commodity like oil is in backwardation, that doesn’t mean that the markets are predicting that its price will fall. It means there is a convenience yield. And in order to decide whether futures markets are creating incentives to store or to sell physical stuff, you have to estimate the convenience yield.

Postscript: While I was writing…

Mark Thoma offers a nice extension of Krugman’s model, showing how monetary policy, by affecting interest rates, would be expected to affect storage.

Yves Smith offers very pointed commentary on futures markets, speculation, and inventory (here and here).

If policymakers want to “do something” about commodity speculation, they should really start investigating passivity on the short side of the market rather than enthusiasm on the long. Given what’s before them, I hope they ignore Michael Masters (ugh!) and Thomas Palley (whom I often like, but yuk), and go with Dean Baker’s suggestion of a Tobin Tax (ht Mark Thoma).

In response to a (somewhat ridiculous) proposal that we “sue OPEC” over high oil prices, Mark Thoma writes:

[I]t’s unlikely that [monopoly power] is the factor behind the run-up in prices. Monopoly power explains the level of prices, i.e. why price is $8 rather than $5, but it doesn’t explain the change in prices, i.e. why the price would change from $8 to $12. There are ways to tell this story, e.g. a war or some other event giving a cartel the cover it needs to raise prices and blame it on external factors, but I don’t think that’s what’s going on in oil markets today, at least I don’t think this is a significant factor behind the oil price increases.

I think there may have been a change over the last few years in the market power of oil producers, for structural reasons. Traditionally, OPEC has suffered from the usual problem that makes large cartels unwieldy: Under agreements to restrain production, members individually have an incentive to cheat and sell larger-than-agreed upon quantities at still artificially high prices. But that assumes that the production quotas are significantly beneath the capacity of most members to produce. More subtly, it also assumes that each country gains by producing more rather than less oil, if cartel prices are maintained. Both of those assumptions may no longer hold.

As the global oil market has grown, demand may have outpaced individual countries’ capacity to supply, either because investment in new projects has not kept pace, or because nations have hit domestic “peak oil”. (See Indonesia for an extreme example.) Other countries may desperately need money in order to fund current spending, so it is widely known they will produce as much as they can, regardless of quotas. Ironically, as long as the total capacity of sure-fire cheaters and constrained suppliers is well below global demand at the cartel’s target price, the certainty of their output may enhance the ability of discretionary producers to control the quantity produced.

It’d always be easier for a cartel of five or six producers to exercise market power than a cartel of, say, thirteen. But that’s especially true when cartel members have little incentive to cheat. Normally, we think of governments as spendthrifts, always eager to spend an extra dime unless constrained by tax revenues or debt markets. That’s obviously a mischaracterization of today’s most important oil producers, whose governments spend far less than the oil revenue they receive. For Saudi Arabia, selling a barrel more of oil is a portfolio choice: revenue from the marginal barrel will be saved, not spent, so the question becomes whether it is wise to shift some of the Kingdom’s current allocation out of oil and into some asset that can be purchased with currency. For countries that have very little non-oil savings, mere diversification would encourage oil sales. It is unwise to have all ones eggs in one basket, and oil producers remember all too well that world prices can go down as well as up. They’d want to store their national wealth in an “efficient portfolio”, one that maximizes their return on risk by including a variety of investments.

But as oil producing nations have accumulated vast reserves of financial assets, switching from oil-in-the ground to stocks, bonds, or bank accounts is no longer so sure a bet. Real interest rates on “safe” dollar assets are currently negative, both in US and home country terms, and the outlook for safe euro assets is uncertain at best. Central banks and sovereign wealth funds of oil-producing nations already hold hundreds of billions of dollars worth of Western financial assets. They might already have reached or exceeded what they view as an optimal allocation of their national wealth into these securities. Of course, producers are still not well diversified, and it’s pretty clear that sovereign wealth funds are looking for alternative assets that might hedge their exposure both to oil and Western paper. But allocating into less liquid, unfamiliar categories of assets is slow work if you want to do it well. Perhaps current oil revenues outstrip oil producers’ capacity to find good investment opportunities, and they view oil-in-the-ground as a better second-best asset than dollars in the bank.

Ten years ago, oil producers did not have vast hoards of dollars and euros, and required oil revenue to meet budgetary needs. World demand was low enough that cheating by OPEC members could corrode producer pricing. It was hard to exercise market power. Now, cheaters don’t matter, and discretionary producers may be indifferent or worse to the prospect of selling a barrel more of oil at current prices.

(In a sense you might not call this market power at all, as price equals marginal cost, that is to oil producers, the assets they can buy for the dollar price of a barrel of oil are worth no more to them than a barrel of oil left in the ground.)

Brad Setser recently noted that…

[T]here are two clear paths that could end the current “oil up, dollar down” pattern.

Weakness in the US economy could drag down global oil demand, pulling both the dollar and oil down. Asia’s 1997-98 crisis led both Asian currencies and the price of oil.

Or a rebound in the US economy could push up the dollar while adding to oil demand. In 2000, a booming US pushed up oil prices and the dollar.

Ironically, a strong, healthy US economy might also push oil prices down, even while increasing US and world demand for oil! The price of oil to discretionary producers is not measured in dollars, but in the future purchasing power of the assets dollars can buy. If oil producers expected US financial assets to appreciate in value more quickly than oil (in terms of what they want to buy), President Bush wouldn’t have to look anyone in they eye to get the producers to invest in new wells. However, if that’s not the case, then the rate of production might be determined more by the political costs of failing to produce than by world demand or current-dollar prices.

But… for US dollar assets to appreciate faster in oil-producer purchasing power than oil itself, those assets would have to represent claims (direct or indirect) on future goods that producers want to buy, that is investment in tradable goods and services. Unfortunately, Brad is probably right to suggest that a “rebound” in the US economy would drive oil prices up, since we’ve come to believe that more GDP is always better, sectoral composition doesn’t matter, and producing tradables is for the little people. Federal stimulus checks might give a zetz to GDP, but in and of themselves they do nothing to make claims on American assets worth buying.

Felix Salmon writes this morining in exasperation:

Let Me Pay to Send Email!

…

What I’d love is some mechanism whereby I could pay “postage” of a few cents, maybe to charity, on selected emails I send. That would be a very strong indication my message was not spam, and should be let through. But I fear coming up with a universal standard for such a mechanism is practically impossible.

A few years ago, a good friend and I were toying with the idea of a tech start-up. (This was post-crash, but we’re both really unreconstructed new economy types.) I offered a proposal that I thought had a very short shelf life. Someone surely would do something like this, soon. Hah!

We would start an e-mail service that would require mail to be “stamped”. You could sign up for it like any e-mail service, but if anyone sent mail to your address and it didn’t have a stamp, it would bounce with an explanation of how to supply postage. No new standards or internet infrastructure would be required.

The receiver of the mail would set the postage rate and get the money. That is, you do not pay a postal service for delivering mail (that’s free in the internet age), you pay the recipient for the burden your correspondence places upon her attention. When mail is delivered, it would include a convenient link whereby you could refund the postage to the sender with a single click. Among frequent correspondents, the postage would be refunded as a matter of course. It would serve as a guarantee of nonabusiveness, but would rarely be paid. Therefore, people could set their postage rates fairly high without losing mail they care about. (One could set-up whitelists of senders whose postage would reimburse automatically, and blacklists of senders whose mail and postage are both refused. Importantly, postage need not vouch for the identity of a sender, but need only associate a letter with an account from which postage has been properly drawn.)

Mail from strangers would not ordinarily be reimbursed, and would serve as a potential source of revenue for people whose attention is in great demand. Although senders would have no guarantee that mail with postage would actually be read, recipients would be encouraged to set a rate at which they’d be willing to give a quick read to a one or two page letter. Famous people could give out real e-mail addresses freely, and use the price mechanism to control the quantity of mail they actually have to sort through. Ordinary blokes would have a means to reach the powerful and famous, at a price. (Of course, senders might often plead poverty and beg that the postage be reimbursed. But mailing would be at senders’ risk. If a recipient is unimpressed with a letter, by default they pocket the cash.)

Also, various kinds of businesses might sprout up using incoming mail as a payments mechanism. These might range from informal consulting gigs (experts on various topics who generally respond to paid questions, that’d be very nice for open-source software support for example) to the email equivalent of 1-900-SEX-LINEs. Whatever. Let a thousand flowers bloom.

A scheme like this could be implemented incrementally, without changing any internet standards. Mail service providers would offer POP, IMAP, or web e-mail access, but would require that incoming mail to have an encrypted header or attachment indicating an account from which postage could be drawn (up to some amount, for a limited period of time, for a specific letter). If the token is present and payment succeeds, the mail is delivered to the user. If not, it is bounced. Mail service providers would earn revenue by taking a fraction of unreimbursed postage payments. Because a monopoly mail service provider is implausible and undesirable, the business model here would be to build software and a payments infrastructure, à la MasterCard, something aspirant competitors would prefer to use than to reconstruct. The goal would be postage interoperability. On the software side, the hardest part would be making postage-payment convenient. One could start decently but imperfectly (e.g. how e-mail-to-fax services bill), but hope to get embedded in popular e-mail clients. Initially, one would market the service as a free, secondary, spam-free e-mail account, and try to get some prominent people to offer publish addresses and postage rates. No one need abandon their traditional, free e-mail accounts, but if managing spam is as costly to others as it is to me, there’d be plenty of incentive to encourage correspondents to migrate in order to reduce the need to monitor open spools.

Legitimate commercial correspondents and opt-in mailing lists would expect to have postage reimbursed, but could not enforce that via the mail system. They would have to establish a contractual relationship prior to mailing, stating that unreimbursed postage payments from certain addresses could be billed back to the recipient. That’s a feature, not a bug. Attention is too scarce a resource to commit as lightly as with a webform checkbox set by default.

Ideas like this have been bouncing around the internet for a long time. I don’t pretend this is particularly novel. I don’t know that it could work. It astonishes me, though, that, as far as I can tell, no one has ever made a serious attempt to do this kind of thing.

Update: In the comments, Richard Serlin points to a very nice, similar proposal by Marshall Van Alstyne. (I know there are more out there, somewhere in the archives of Slashdot.) In Alstyne’s proposal the recipient opts to take, rather than opting to reimburse, which might be a better “choice architecture“. That way you don’t piss your friends off just by having forgetten to click a link.

What distinguishes a speculator from a hedger? Here’s the New York Times:

Unlike hedgers — the farmers, miners, refineries and other commercial interests that actually make or use the commodities themselves — the speculators, like day traders in the stock market, are simply trying to profit from changing prices.

But that’s not really right. Conceptually, a hedger is a party trying to shed risk, usually accepting some cost to do so, while a speculator willingly takes on risk, hoping to profit.

If we take nominal dollars as investors’ unit-of-account, then all noncommercial interest in commodities is “speculation”, as the Times implies. People are pouring money into commodities because they believe commodity prices will rise in US dollar terms. Since holding cash is risk-free (in nominal dollar terms), all investment is speculation unless it’s offsetting some commercial risk.

But if we more realistically view investors’ planned consumption bundles as their unit-of-account, the recent interest in commodities is better characterized as hedging than speculation. Investors perceive the value of currency to be more volatile than stored commodities, relative to the goods and services they hope to consume. It would be inefficient for investors to store commodities directly, so they hire professionals to store on their behalf by purchasing financial futures. (In properly functioning futures markets, when more money wants to go long than short, an invisible hand seeks out those capable of efficient storage, and compels them to fill warehouses in order to meet the excess demand.)

What Joe Lieberman proposes to do, then, is best understood not as barring speculation by institutional investors, but as barring hedging, as forcing investors to accept risks that they would prefer to shed.

Yves Smith writes that Senator Lieberman’s proposal is “a Nixon-goes-to-China moment”. I am wrong far more often than Yves Smith is, but I’m gonna go out on a limb here and say she’s mistaken. The Senator fron Hedgefundistan is acting very much on behalf of his constituents. Smith writes:

Opponents may argue that this will simply drive investing in commodities overseas. Perhaps, but funds regulated under the Investment Company Act of 1940 (most US fund managers) don’t have that sort of latitude, and ERISA investments could similarly be reined in quite easily. And it’s US investors, plagued by (until recently) an ever falling dollar who have had particularly strong reasons to look to a hedge like commodities.

As a move to drive any speculative froth out of commodities, this one isn’t bad (but one wonders how all those commodities index funds get unwound). Although some have called for increases on margins at commodities exchanges, that hurts commercial actors as well as speculators. A move like this focuses on the underlying issue more directly.

Goldman in particular would suffer, since as the biggest manager of commodities funds based on its index, GSCI, it not only earns fees, but as we have discussed elsewhere, earns even more from an unsavory but hugely profitable practice called “date rape” around the monthly futures contract roll.

Now before the wealth-holding class howls that they’ve just been done a dirty by being deprived of inflation protection, there is an asset class that, unlike commodities, supports productive investment. and provides inflation protection, namely, infrastructure investments. The cash flow from infrastructure projects (toll roads, airports) goes up over time, as do the payouts, so they have fairly secure cash flow that increases over time. Although there is some debate about how to view them, they seem closest to an inflation-indexed bond (although any investor would need to study the ability of the enterprise to increase charges versus the drivers of operating expenses).

Many investment funds may be prohibited by charter or regulation from participating in overseas commodity markets, but Senator Lieberman’s hedge fund constituents and their wealthy accredited investors are not. The “wealth-holding class” would evade these restrictions quite easily, by funneling money through Connecticut businesses. This would be a growth-enhancing regulation for Stamford.

Meanwhile, retirement funds and retail ETF investors would be stuck with currency-denominated securities, and forced to bear any loss of purchasing power. Infrastructure as an asset class might or might not be a reasonable inflation hedge, as might stock (in the long run, equities are said to pass through inflation), TIPS, or any number of other assets. But that’s fundamentally a decision for individuals to make. If infrastructure is a good choice, let the hedge funds buy it. But so long accredited investors (and savvy individuals with direct futures market accounts) have access to commodity exposure, it is inequitable to prevent the beneficiaries of ordinary investment funds from enjoying the same.

The United States economy is suffering the aftermath of poor aggregate investment decisions over a period of many years. Losses will have to be taken on those investments. The “wealth-holding class” responsible for the misdirection of capital will do what it can to shift losses to dispersed and relatively powerless little guys. I’d be glad to see the government take a more active role in addressing America’s economic crisis. But most of the proposals out of Washington so far, including this idea from Senator Lieberman, give options to banks and wealthy investors while shoving costs and constraints onto everyone else. Trying to address the “commodity bubble” by restricting so-called speculation is a fool’s game. If it’s a bubble pop it, if it’s a response to real risks, address those. Blaming speculators is like combating global warming by banning thermometers.

FD: I’m an evil speculator, but as an individual who trades futures directly, Senator Lieberman’s proposal wouldn’t prevent me from escaping the little people’s inflation. That said, the only commodities I’m long are precious metals. I’m short Ag comodities via a retail ETF. I lose money all the time, so taking anything I say as investment advice is just dumb.

If you think $135 oil is a speculative bubble, that the only basis for current prices is want of a pin, here’s a plan. If you’re right, there’s a market failure. Those with access to physical oil are accommodating the bubble for some reason, when they could, should in theory, sell forward in quantity and insist upon delivery, forcing speculators who cannot accept physical oil to close their positions at desperation prices. Note you don’t have to overwhelm all the specs. Prices are set at the margin. You just have to sell with intent to deliver contracts representing somewhat more than demand for actual delivery to force oil off a cliff and crush the specs like bugs. If private arbitrageurs won’t do this — perhaps those who can, don’t, because they benefit more from high headline oil prices than they lose from foregoing a one-time arb &mdash then perhaps government should step in.

The US Strategic Petroleum Reserve could sell $135 oil forward in very large quantities, and refuse to close its contracts prior to delivery.

If you are right, and oil is an ordinary speculative bubble, then prices will fall sharply, and the petroleum reserve will be able to recover all the oil it sold cheaply, turning a profit for taxpayers.

But, if you are wrong, and oil prices are due to either current fundamentals or informed speculation on future supply and demand, then players interested in consuming or storing the product will step in as prices begin to fall and start buying. Prices would fall a little, but the drop would be transient, and the petroleum reserve would take a loss when it eventually repurchases to replenish.

It’d be a gamble. But if you think this is a bubble, a quick Federal pricking would be far less damaging public policy than curtailing unleveraged speculation. If you’re not so sure it’s a bubble, if you think it’s possible that current or future supply and demand justify current prices, then you should definitely not be banning speculators, who are doing the good work dissuading us from squandering what is precious. If you think current prices are a monetary phenomenon, that selling oil forward trades a valuable commodity for depreciating paper, then you don’t think this is a bubble at all, and limiting speculation is just a way of preventing would-be speculators from evading an inflation tax and spreading disquieting news.

I don’t know whether current oil prices a speculative bubble or not. Maybe, maybe not. Maybe the best way to find out is with the help of a nice long pin.

While chatting with a commenter on the previous post, I went back to the Mathematica notebook where I had played with the numbers, and found an error in my arithmetic that is, as they say, “material”. I erroneously used 68%, rather than 67%, as the late 90s participation rate, when I asserted that unemployment would be 8% today if participation returned to previous levels. The correct value is 6.6%.

That is, if an additional 0.8% of the “civilian noninstutional population” became active job seekers, but no net new jobs were created, the reported unemployment rate would be 6.6%. (The numbers, which hopefully I’ve correctly transcribed for a change, are May 2008 data from the June 6 release of BLS employment situation, Table A-1.) That’s still a big jump from 5.5%, but it’s a far cry from 8%, which sounds like a nasty recession.

To say I regret the error would understate the red-faced heart-thumpingness of the thing. Sorry!

Much of the chatter surrounding the latest BLS release has focused on a spike in the denominator of the unemployment statistic, the fraction of the population either working or actively looking for work. Courtesy of the indispensible FRED…

About a year ago, David Altig (whose macroblogging I miss very much) wrote the following:

[Since 2000] you would be justified in claiming a broad-based decline in the number of people choosing to participate in U.S. labor markets. But I use the word “choosing” intentionally, as I’m convinced that the post-2000 changes in labor force participation rates (or employment-to-population ratios, if you like) reflect trends that are largely independent of the business cycle.

Much turns on the question of why people chose not to participate in the labor force this decade. A “business cycle” explanation, as I read Altig, would mean that people left the labor force because there weren’t employment opportunities. They couldn’t find a job, and became “discouraged workers”, in the lingo. I agree with Altig that this is unlikely. However, unemployment statistics (very uneconomically) ignore price, and stagnant real wages over the period undoubtedly had something to do with the decline in participation. People chose not to work because they decided the money wasn’t worth their time.

But it’s also important to consider a credit cycle explanation for why people left the workforce. One has the luxury of choice when one can afford to do without employment. During a credit expansion, many people have that luxury, because one can live off of borrowing and asset appreciation. You can quit your shitty job and withdraw some home equity while you write the great American novel, focus on your music, or raise your children. You can go to school, even though you lack savings, because student loans are plentiful.

But when credit conditions tighten and asset prices fall, work becomes less optional. Quitting the rat race and pursuing your passion starts to recall the phrase “starving artist”, and not in a charming way. Dad might decide he needs a job to make ends meet, even if that means putting the kids in day care.

Some argue that the US economy is structurally immune from the wrenching spikes in unemployment that used to accompany recessions, because employment has transitioned from volatile manufacturing to more mellow services. See, for example, this excellent analysis from Calculated Risk. CR chooses 8% unemployment as his threshold for a “severe” recession. But the US economy need not lose a single job more to bring unemployment to that level. If participation rose back to the levels of the late 90s without a commensurate increase in new jobs, we’d be there already we’d be at 6.6% unemployment right now. [Note: In my original calculations, I mistakenly entered 68%, rather than 67%, as the late 90s participation rate, significantly exaggerating the effect. My apologies for the error!]

When we ended welfare as we know it, back in the nineties, the slogan “Choose to work” might have captured the spirit of the times. It’s ironic that more than a decade later, the apparent health of the American economy depends largely on how many people continue to choose not to work, now that the credit spigot has dried up.

A very good friend of mine is putting together a venture capital fund devoted to “double bottom line” companies in financial services. In particular, this fund will invest in new business models for providing services to the “underbanked” (whom my friend quaintly insists on referring to as poor people). He’s looking for people with a strong background in finance and investment who would be into this kind of thing. The job would be in New York. If you’re interested, please write something about yourself to doublebottomline@yahoo.com. (Please don’t write to me, I don’t know anything more than I’ve already written.)

It’s easy to be cynical about all this, and Interfluidity ain’t a job site, but this is someone I know, and what he does he does well. My apologies for the ad-ish-ness. I promise not to make a habit of it.